人教版八年级上册数学课本重点难点是什么？

校园之窗 2025年12月10日 22:25:27 99ANYc3cd6 1 0

人教版数学八年级上册教材概览

人教版数学八年级上册是初中数学承上启下的关键一册,它不仅巩固了七年级所学的知识，更引入了许多重要的数学思想和方法，为后续的九年级学习乃至整个高中阶段的数学学习打下坚实的基础。

教材结构与主要章节

本册教材共包含 十一章 内容，大致可以分为 “数与代数”、“图形与几何”、“统计与概率” 三大板块。

（图片来源网络，侵删）

第一部分：数与代数 (核心章节)

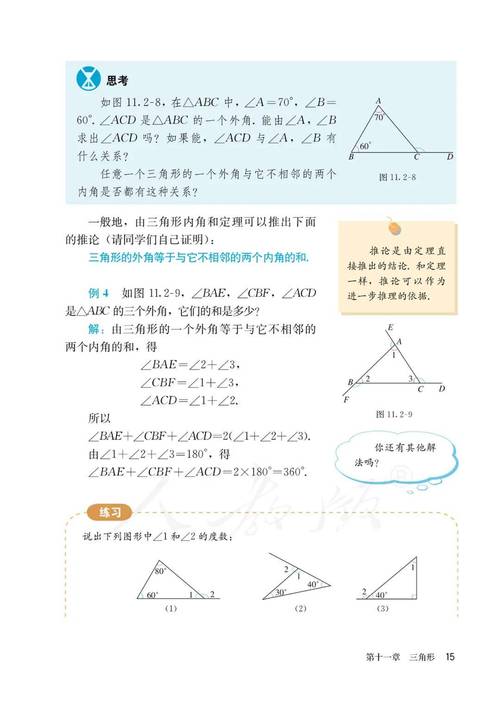
第十一章三角形
- 地位：本章是整个“图形与几何”部分的开篇和基础，是后续学习全等三角形、轴对称、四边形等内容的前提。
- 核心知识点：
  - 三角形的边：三边关系定理（两边之和大于第三边，两边之差小于第三边）。
  - 三角形的角：内角和定理（180°），外角定理（等于不相邻的两个内角和）。
  - 多边形的内角和与外角和：内角和公式 (n-2)×180°，外角和恒为 360°。
- 数学思想：初步体会分类讨论思想和方程思想。
第十二章全等三角形
- 地位：本章是初中几何证明的入门和核心，是学习几何证明方法的基石。
- 核心知识点：
  - 全等三角形的性质：对应边相等，对应角相等。
  - 全等三角形的判定：
    - SSS (边边边)
    - SAS (边角边)
    - ASA (角边角)
    - AAS (角角边)
    - HL (斜边直角边 - 仅限Rt△)
  - 角平分线的性质：角平分线上的点到角两边的距离相等。
- 数学思想：几何证明是本章的重中之重，需要掌握规范的证明格式和逻辑推理过程。
第十三章轴对称
（图片来源网络，侵删）
- 地位：从“运动”的角度研究图形，是几何学习的重要视角。
- 核心知识点：
  - 轴对称图形与图形的轴对称的概念区别与联系。
  - 轴对称的性质：对应线段相等，对应角相等，对称轴是任何一对对应点所连线段的垂直平分线。
  - 线段的垂直平分线：性质定理和判定定理。
  - 等腰三角形：性质（“三线合一”）和判定。
  - 等边三角形：性质和判定。
  - 最短路径问题：利用轴对称解决“将军饮马”类问题。
- 数学思想：数形结合思想、转化思想（将复杂问题转化为简单的轴对称问题）。
第十四章整式的乘法与因式分解
- 地位：代数运算的核心，是后续学习分式、二次方程的基础。
- 核心知识点：
  - 整式的乘法：
    - 幂的运算性质（同底数幂相乘、幂的乘方、积的乘方）。
    - 单项式与单项式、多项式相乘。
    - 乘法公式（重点）：平方差公式 (a+b)(a-b) = a² - b²，完全平方公式 (a±b)² = a² ± 2ab + b²。
  - 因式分解：
    - 提公因式法。
    - 公式法（平方差公式、完全平方公式）。
    - 十字相乘法（选学，但非常重要）。
- 数学思想：整体思想、逆向思维（乘法与因式分解互为逆运算）。
第十五章分式
- 地位：小学分数的推广和深化，是学习分式方程和函数的基础。
- 核心知识点：
  - 分式的基本性质：约分和通分。
  - 分式的运算：加、减、乘、除、乘方。
  - 分式方程：定义、解法（去分母转化为整式方程）及验根（必须步骤！）。
  - 整数指数幂：负整数指数和零指数幂的意义。
- 数学思想：类比思想（类比分数学习分式）、转化思想（将分式问题转化为整式问题）。

第二部分：图形与几何 (应用与深化)

第十六章二次根式
（图片来源网络，侵删）
- 地位：为学习勾股定理和一元二次方程做准备。
- 核心知识点：
  - 二次根式的概念和性质（√a ≥ 0）。
  - 二次根式的乘除法。
  - 二次根式的加减法（先化简，后合并同类项）。
- 数学思想：运算能力、化简思想。
第十七章勾股定理
- 地位：揭示直角三角形三边关系的“第一定理”，是几何计算的重要工具。
- 核心知识点：
  - 勾股定理（a² + b² = c²）及其证明。
  - 勾股定理的逆定理（判断一个三角形是否为直角三角形）。
  - 勾股定理的实际应用（最短路径问题、航海问题等）。
- 数学思想：数形结合思想、方程思想。

第三部分：统计与概率 (初步)

第十八章数据的分析
- 地位：对七年级“数据的收集与整理”的深化，学习如何用数字来描述数据的集中趋势和波动情况。
- 核心知识点：
  - 平均数：算术平均数和加权平均数。
  - 中位数和众数：描述数据的集中趋势。
  - 方差：描述数据的波动大小（离散程度），方差越大，数据越不稳定；方差越小，数据越稳定。
  - 用样本平均数/方差估计总体平均数/方差。
- 数学思想：统计思想、样本估计总体的思想。

本册教材的重点与难点

重点：
1. 全等三角形的判定与证明：这是几何的入门，必须熟练掌握。
2. 轴对称的性质及其应用：特别是等腰三角形的性质和“最短路径问题”。
3. 整式的乘法与乘法公式：运算是基础，公式是核心。
4. 分式的运算与解分式方程：注意运算顺序和验根。
5. 勾股定理及其应用：直角三角形的“灵魂”。
难点：
1. 几何证明的逻辑推理：如何从已知条件出发，选择合适的判定定理进行证明，是初学者的最大难关。
2. 乘法公式的灵活运用：特别是完全平方公式，容易漏掉中间项 2ab。
3. 分式的混合运算：运算顺序复杂，容易出错。
4. 方差的理解：方差的意义比较抽象，需要结合实例来理解。