八年级下册等腰三角形教案如何突破教学难点？

人教版八年级下册数学《等腰三角形》第一课时教案

教学目标

1. 知识与技能:

   • 理解并掌握等腰三角形的概念,能准确识别等腰三角形。
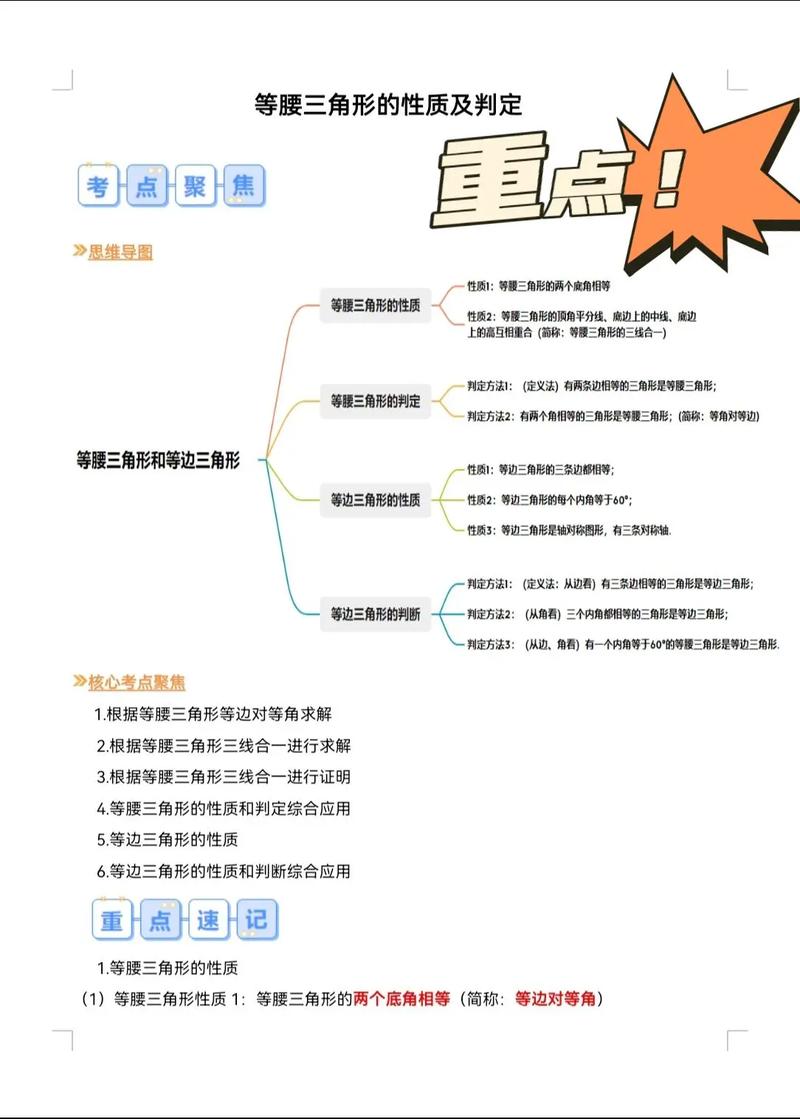
   • 掌握等腰三角形的性质：“等边对等角”和“三线合一”。
   • 能够运用等腰三角形的性质进行简单的计算和证明。

2. 过程与方法:

   
   （图片来源网络，侵删）
   • 通过对折、测量、猜想、验证等动手操作和合作探究活动，体验几何结论的发现过程，培养学生的观察、归纳、猜想和验证能力。
   • 在性质的证明和应用中,初步体会“转化”的数学思想，即将未知问题转化为已知问题（如将三角形问题转化为两个直角三角形的问题）。

3. 情感态度与价值观:

   • 在探索活动中,激发学习数学的兴趣，感受几何图形的对称美。
   • 通过合作交流,培养学生的团队协作精神和语言表达能力。
   • 培养学生严谨的治学态度和逻辑推理能力。

教学重难点

• 教学重点:

  等腰三角形性质的探索、理解和应用。

• 教学难点:

  
  （图片来源网络，侵删）
  • 等腰三角形“三线合一”性质的准确理解和区分。
  • 性质证明过程中辅助线的添加思路（作顶角平分线/底边上的中线/底边上的高）。

教学方法

• 引导发现法、合作探究法、讲练结合法。

教学准备

• 教师: 多媒体课件（PPT）、剪刀、彩纸、量角器、直尺。
• 学生: 剪刀、彩纸、量角器、直尺、练习本、笔。

教学过程

(一) 创设情境，引入新课 (约5分钟)

1. 实物展示:

   • 教师出示一张长方形的彩纸,提问：“同学们，这张纸是什么形状？它有什么特点？”（引导学生说出：对称轴）。
   • 教师提问：“如果我们想剪出一个具有对称轴的三角形，应该怎么剪？”
   • 请一名学生上台尝试：将纸对折，然后沿一条直线剪开，展开后得到一个三角形。

2. 揭示课题:

   • 教师展示剪出的三角形,提问：“这个三角形有什么特点？”（引导学生观察，发现两边相等）。
   • 教师总结：像这样有两条边相等的三角形，我们称之为等腰三角形。
   • 板书课题：19.1.2 等腰三角形（第一课时）

(二) 动手操作，探究新知 (约15分钟)

等腰三角形的概念

1. 定义与画法:

   • 教师在黑板上画一个等腰三角形△ABC，其中AB = AC。
   • 定义: 有两条边相等的三角形叫做等腰三角形。
   • 相关概念:
     • 相等的两边叫做腰。（AB和AC）
     • 另外一边叫做底边。（BC）
     • 两腰所夹的角叫做顶角。（∠A）
     • 底边与腰所夹的角叫做底角。（∠B和∠C）

2. 对称性:

   • 提问：“我们剪出的等腰三角形是轴对称图形吗？对称轴是哪条线？”
   • 引导学生回答：是轴对称图形，对称轴是顶角A的平分线所在的直线。

等腰三角形的性质

1. 猜想“等边对等角”

   • 活动1：测量与猜想
     • 学生拿出自己课前准备的等腰三角形纸片。
     • 使用量角器分别测量两个底角的度数,并记录下来。
     • 与同桌交流测量结果,你发现了什么？
   • 猜想: 等腰三角形的两个底角相等。
   • 板书：性质1：等腰三角形的两个底角相等（简称：等边对等角）。

2. 验证猜想（性质1的证明）

   • 问题: 我们通过测量发现了这个规律，但数学结论需要严格的逻辑证明，如何证明∠B = ∠C呢？
   • 引导分析:
     • 我们要证明的是两个角相等,目前学过的能证明角相等的方法有哪些？（全等三角形的对应角相等、平行线的内错角/同位角相等、等量代换等）。
     • 在这个三角形内部,没有现成的平行线，我们能否构造出全等的三角形呢？
     • 引出辅助线的思想：作一条线，将△ABC分成两个三角形。
   • 证明过程（师生共同完成）：
     • 作法： 作顶角∠BAC的平分线AD，交底边BC于点D。
     • 求证： ∠B = ∠C
     • 证明：
       • 在△ABD和△ACD中，
       • { AB = AC (已知)
       • { ∠1 = ∠2 (AD是角平分线)
       • { AD = AD (公共边)
       • ∴ △ABD ≌ △ACD (SAS)
       • ∴ ∠B = ∠C (全等三角形的对应角相等)
   • 教师强调: 辅助线AD不仅是角平分线，我们还可以证明它也是底边BC上的中线和高，这就是等腰三角形另一个非常重要的性质。

3. 探究“三线合一”

   • 活动2：观察与归纳
     • 回到刚才的证明过程,既然△ABD ≌ △ACD，那么对应的边和角有什么关系？
     • 学生回答：BD = CD, ∠ADB = ∠ADC。
   • 归纳性质:
     • 因为BD = CD，所以AD是底边BC的中线。
     • 因为∠ADB = ∠ADC，又因为这两个角相邻且互补，所以它们都等于90°，所以AD也是底边BC的高。
     • 板书：性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（简称：三线合一）。
   • 辨析与强化:
     • 强调: “三线合一”指的是同一条线（顶角的平分线）同时具有另外两个身份（底边上的中线和高）。
     • 提问: 如果已知等腰三角形底边上的中线，它是否也具备另外两个身份？（是）底边上的高呢？（是）
     • 用几何语言表示:
       • 在△ABC中，AB=AC
       • ① ∠1 = ∠2 ⇒ AD⊥BC, BD=CD
       • ② BD=CD ⇒ ∠1 = ∠2, AD⊥BC
       • ③ AD⊥BC ⇒ ∠1 = ∠2, BD=CD

(三) 例题讲解，巩固应用 (约15分钟)

例1：基础计算与证明

如图,在△ABC中，AB = AC，D是BC边上的中点。 (1) 若∠B = 40°，求∠C和∠BAD的度数。 (2) 求证：AD⊥BC。

(此处应有图形)

解题思路分析: (1) 分析:

• 已知AB=AC，根据“等边对等角”，可以直接得出∠C的度数。
• 要求∠BAD，可以观察到△ABD也是一个等腰三角形（AB=AC, BD=CD），BAD = ∠B = 40°。
• 或者,利用“三线合一”，AD是底边上的高，ADB=90°，在△ABD中，∠BAD = 180° - ∠B - ∠ADB = 180° - 40° - 90° = 50°。（这里可以引导学生发现两种思路，并比较优劣）
• 解答:
  • (1) ∵ AB = AC (已知)
  • ∴ ∠C = ∠B = 40° (等边对等角)
  • 又∵ D是BC的中点 (已知)
  • ∴ BD = CD
  • 又∵ AB = AC (已知)