八年级上册数学轴对称课件重点难点是什么？

八年级上册数学《轴对称》全攻略：从入门到精通，课件、难点、考点一网打尽！

Meta描述： 还在为八年级上册数学《轴对称》章节头疼？本文作为资深教师总结，详细解析轴对称的定义、性质、作图及最短路径问题，并附赠高质量课件思路与学习方法，助你攻克难关,轻松拿捏考点！

---

引言：为什么《轴对称》是八年级数学的“分水岭”？

亲爱的同学们、各位家长朋友们,大家好！

八年级上册的数学学习，是一个承上启下的关键时期，而其中，《轴对称》这一章节，不仅是几何学习的重点，更是许多同学从“形象思维”迈向“抽象逻辑思维”的“分水岭”，它看似简单，实则蕴含着丰富的数学思想和方法，一个高质量的《轴对称》课件，不仅能帮助你直观理解概念，更能让你在解题时思路清晰、游刃有余。

我将作为你的专属数学导师，带你深度剖析《轴对称》的全部内容，从核心知识点到高频考点，再到如何利用课件高效学习，为你呈上一份全方位的“通关秘籍”。

---

第一部分：核心知识点精讲——构建你的知识大厦

在接触课件之前，我们必须先搭建起坚实的知识框架，一个优秀的课件,必然是对这些核心知识点的完美呈现。

什么是轴对称图形？

• 定义： 如果一个图形沿某一条直线折叠，直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形，这条直线就是它的对称轴。
• 课件呈现建议： 课件中应大量使用动态GIF或视频演示，展示一个蝴蝶、一个“喜”字、一个等腰三角形沿某条直线折叠后完美重合的过程。视觉冲击力是帮助学生建立概念的第一步。
• 生活实例： 建筑物（如天安门）、交通标志、剪纸艺术、人体等,都是轴对称图形的绝佳例子。

轴对称与轴对称图形的区别与联系

这是学生最容易混淆的概念,课件必须重点突出。

特征	轴对称	轴对称图形
对象	两个图形	一个图形
运动	一个图形沿某条直线翻折，与另一个图形重合。	图形自身沿某条直线折叠，两旁部分重合。
结果	形成两个全等的图形。	图形自身具有对称性。
联系	轴对称的两个图形看作一个整体，就是一个轴对称图形。	把一个轴对称图形位于对称轴两旁的部分看作两个图形，它们关于对称轴轴对称。

• 课件呈现建议： 使用对比表格，并配以动画，左边动画演示两个三角形关于直线l对称（轴对称），右边动画演示一个等腰三角形沿高折叠（轴对称图形）,最后用箭头清晰地展示它们之间的转化关系。

轴对称的性质——解题的“金钥匙”

这是本章的核心,也是课件需要浓墨重彩的部分。

• 性质1：关于某条直线对称的两个图形是全等形。
  • 解读： 这是基础，意味着对应边相等,对应角相等。
• 性质2：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线
  • 解读： 这是作图和找对称点的理论依据，课件中应通过动画，反复演示“连接对称点 -> 作线段 -> 作中垂线”的过程。
• 性质3：两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么交点一定在对称轴上。
  • 解读： 这个性质在解决复杂问题时非常有用，课件可以设置一个探究环节,让学生自己拖动图形发现这个规律。

---

第二部分：高频考点与解题技巧——从“学会”到“会考”

知识点是基础，考点是方向，一个优秀的课件,必须包含对这些考点的针对性训练。

作图题——手绘对称图形

• 题型： 作一个点、一条线段、一个三角形关于某条直线的轴对称图形。
• 解题技巧：
  1. 找关键点： 对于多边形,通常是找其顶点。
  2. 作垂线： 过关键点作对称轴的垂线。
  3. 截取等长： 在垂线上，从对称轴开始，在另一侧截取与关键点到对称轴距离相等的线段,找到对称点。
  4. 连线成图： 依次连接各对称点。
• 课件呈现建议： 制作分步交互式动画，点击“第一步”，只显示“找关键点”和“作垂线”；点击“第二步”，显示“截取等长”；最后点击“完成”，显示整个图形,这能让学生一步步掌握方法。

最短路径问题——“将军饮马”模型

这是本章的难点和压轴题常客,也是最能体现数学思想的部分。

• 问题模型： 在直线l（如河岸、公路）两侧，分别有A、B两个点（如村庄、军营），现在要在l上建一个点P，使得AP + BP最短。
• 解题思想： 转化思想，利用轴对称，将“折线”转化为“直线”。
• 解题步骤：
  1. 作对称： 作出点A关于直线l的对称点A'。
  2. 连线段： 连接A'B,与直线l的交点即为所求的点P。
  3. 原理： 根据轴对称性质，AP = A'P，所以AP + BP = A'P + BP，在连接A'和B的所有线段中，线段A'B最短。
• 课件呈现建议： 这是课件必须有的“杀手锏”功能，通过动画演示：
  • 动态展示点P在直线上移动时，AP+BP的长度变化。
  • 当P移动到特定位置时，AP+BP的长度等于A'B的长度。
  • 用不同颜色突出显示AP和A'P的相等关系，让学生直观理解“转化”的妙处。

---

第三部分：如何利用课件高效学习？——给你的学习加点“料”

课件不是电影，不能只看不练，高效利用课件,才能事半功倍。

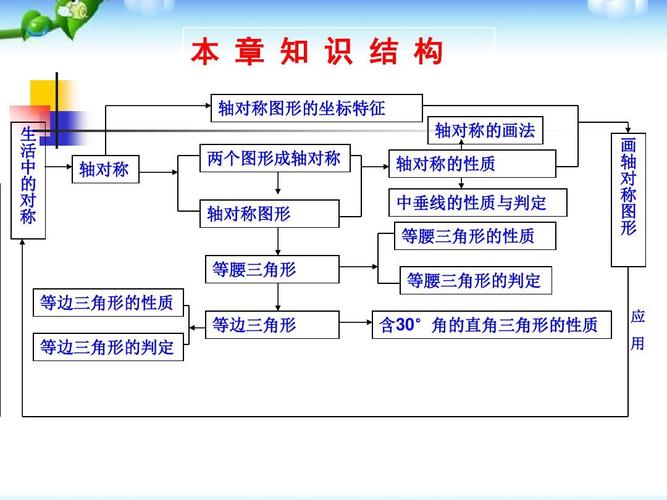
1. 课前预习，带着问题听课： 课前花15分钟，快速浏览课件的核心概念和动画演示，找出自己看不懂的地方，标记下来,上课时重点听老师讲解。
2. 课中同步，化抽象为具体： 老师讲到某个知识点时，回看课件中的动态演示，讲到垂直平分线，就再看一遍对应点的连线动画,让课件的视觉记忆辅助你的听觉记忆。
3. 课后复习，主动探究而非被动观看：
   • 遮盖练习： 看着课件上的图形,自己尝试复述定义和性质。
   • 变式思考： 课件上有一个“将军饮马”模型，你可以思考：如果A、B两点在直线同侧，怎么解决？如果换成求|AP - BP|的最大值,又该如何？
   • 举一反三： 课件上的例题是基础，你要尝试自己改编题目,或者做课件配套的变式练习题。

---

第四部分：如何获取一份优质的《轴对称》课件？

一份好的课件是学习的催化剂，市面上资源众多,如何甄别？

• 深度： 优质课件不仅包含知识点，更有思想方法的提炼（如转化思想、数形结合思想）和中考真题的链接。
• 关注交互性： 优先选择带有可拖动、可点击、分步演示功能的课件,而不是静态的图片集合。
• 关注配套资源： 是否有教案、学案、习题等配套资源？这决定了课件能否真正落地使用。

（此处可根据实际情况，插入您自己制作的课件资源链接，或推荐一些可靠的、符合上述标准的资源平台，如XX教育网、XX教师云空间等，并引导用户搜索“八年级上册数学轴对称课件 互动版”等关键词。）

---

同学们，《轴对称》的世界充满了美与智慧，它教会我们的，不仅仅是几何知识，更是一种化繁为简、化曲为直的数学思想，希望这篇详尽的分析，能帮助你更好地理解《轴对称》的魅力。

最好的课件，永远是你经过思考后，亲手整理和总结出的那份笔记，希望这份攻略能成为你构建这份“完美课件”的蓝图。

学习之路，道阻且长，行则将至，加油！