人教版八年级上册数学练习题答案在哪找？

人教版八年级上册数学核心章节练习题

第一章 三角形

填空题

1. 一个三角形的两边长分别为 3 和 7，则第三边的长度 x 的取值范围是 ____。
2. 在 △ABC 中，∠A = 50°，∠B = ∠C，则 ∠C = ____。
3. 等腰三角形的一个角为 80°，则它的另外两个角的度数分别为 ____ 或 ____。
4. 一个多边形的内角和是 900°，则这个多边形是 ____ 边形。

选择题 5. 下列长度的三条线段能组成三角形的是 ( ) A. 2, 3, 5 B. 3, 4, 8 C. 5, 6, 10 D. 4, 4, 9 6. 下列图形中，具有稳定性的是 ( ) A. 正方形 B. 长方形 C. 三角形 D. 平行四边形 7. 下列说法中，错误的是 ( ) A. 三角形的三条高所在的直线一定相交于一点 B. 三角形的一个外角等于和它不相邻的两个内角的和 C. 三角形的一个外角大于任何一个内角 D. 钝角三角形有两条高在三角形外部

解答题 8. 如图，在 △ABC 中，AD 是 BC 边上的高，AE 是 ∠BAC 的平分线，∠B = 40°，∠C = 60°，求 ∠DAE 的度数。 (解题思路：先求出 ∠BAC，再利用角平分线性质求出 ∠BAE，最后在直角三角形 ABD 中求出 ∠BAD，进而求解。)

---

第二章 全等三角形

填空题 9. 如图，△ABC ≌ �DEF，AB = DE，∠A = 40°，则 ∠F 的度数为 ____。 (解题思路：全等三角形对应角相等，找到 ∠F 的对应角。) 10. 如图，点 E, F 在 BC 上，BE = CF，AB = DC，要证明 △ABF ≌ △DCE，可以添加的一个条件是 ____ (只需写出一个)。 (解题思路：利用 BE=CF 可得 BF=CE，结合 AB=DC 和公共角 ∠B=∠C，可用 SAS 证明。)

选择题 11. 下列条件中，不能判断两个直角三角形全等的是 ( ) A. 两条直角边对应相等 B. 斜边和一条直角边对应相等 C. 斜边和一个锐角对应相等 D. 两个锐角对应相等 12. 如图，AC = AD，BC = BD，下列结论中不正确的是 ( ) A. ∠1 = ∠2 B. AB 垂直平分 CD C. AB 平分 ∠CAD D. △ABC ≌ △ABD (用 AAS 证明)

解答题 13. 如图，点 A, C, F, D 在同一条直线上，AF = DC，AB = DE，AB ∥ DE，求证：△ABC ≌ △DEF。 (解题思路：由 AB ∥ DE 得 ∠A = ∠D，结合 AF=DC 可得 AC=DF，再用 SAS 证明全等。) 14. 如图，在 △ABC 中，∠ACB = 90°，AC = BC，直线 MN 经过点 C，且 AM ⊥ MN 于 M，BN ⊥ MN 于 N，求证：MN = AM + BN。 (解题思路：此题为经典“一线三等角”模型，可过点 C 作 CE ⊥ BN 于 E，证明 △AMC ≌ △CNE (AAS)，从而得到 AM=CN，MC=NE，进而 MN=MC+CN=MC+AM=AM+BN。)

---

第三章 轴对称

填空题 15. 点 P(-2, 3) x 轴对称的点的坐标是 ____。 16. 等腰三角形有两条对称轴，则它的顶角为 ____ 度。 17. 如图，△ABC 中，DE 是 AC 的垂直平分线，若 AB = 8 cm，BC = 5 cm，则 △BDC 的周长是 ____ cm。 (解题思路：利用垂直平分线性质，AD=DC，所以周长 = BD + DC + BC = BD + AD + BC = AB + BC = 8 + 5 = 13 cm。)

选择题 18. 下列图形中，是轴对称图形但不是中心对称图形的是 ( ) A. 平行四边形 B. 矩形 C. 菱形 D. 等腰三角形 19. 如图，在 △ABC 中，AB = AC，∠BAC = 120°，AD 是 BC 边上的高，DE ⊥ AB 于 E，DF ⊥ AC 于 F，若 AD = 4，则 DE + DF 的值为 ( ) A. 2 B. 3 C. 4 D. 5 (解题思路：连接 CD，利用面积法，S△ABC = S△ABD + S△ACD，1/2 AB (DE+DF) = 1/2 AB AD，因为 ∠B=∠C=30°，AD=4，AB=8，代入可得 DE+DF=AD=4。)

解答题 20. 如图，在 △ABC 中，AB = AC，∠BAC = 40°，点 D 为 BC 边上一点，将 △ABD 沿 AD 翻折，得到 △AED，求 ∠EDC 的度数。 (解题思路：利用轴对称性质，∠EAD = ∠BAD，∠E = ∠B，先求出 ∠B = (180°-40°)/2 = 70°，设 ∠BAD = x，则 ∠EAD = x，在 △ABD 中，∠ADB = 180° - ∠B - ∠BAD = 180° - 70° - x = 110° - x，因为 ∠ADB 和 ∠EDC 是对顶角，∠EDC = 110° - x，在 △AED 中，∠EAD = x，∠E = 70°，∠AED = 180° - x - 70° = 110° - x。∠EDC = ∠AED。)

---

第四章 整式的乘除与因式分解

填空题 21. 计算：(-2x²y)³ = ____。 22. 计算：(a - 2b)(a + 2b) = ____。 23. 计算：(x + 2)² = ____。 24. 因式分解：ax² - 4ay = ____。

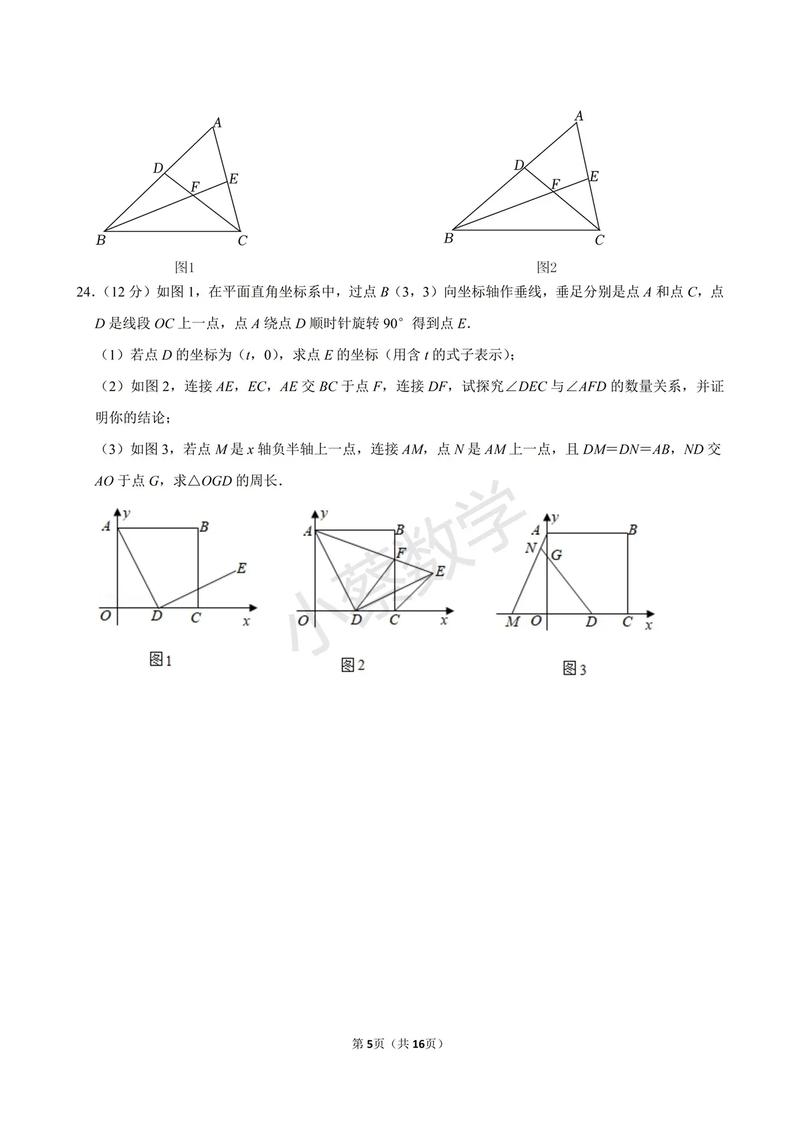
选择题 25. 下列运算正确的是 ( ) A. a³ · a² = a⁶ B. (a²)³ = a⁵ C. (a + b)² = a² + b² D. a⁴ ÷ a² = a² (a ≠ 0) 26. 下列多项式能用平方差公式分解因式的是 ( ) A. x² + y² B. -x² + y² C. -x² - y² D. x² - 2xy + y²

解答题 27. 计算：(2x - 3y)² - (2x + 3y)(2x - 3y) (解题思路：先利用完全平方公式和平方差公式展开，再合并同类项。) 28. 先化简，再求值：(a + 2b)² - (a + 2b)(a - 2b)，a = 1，b = -2。 (解题思路：先利用公式化简，再代入数值计算。)

---

第五章 分式

填空题 29. 当 x = ____ 时，分式 2/(x-1) 无意义。 30. 化简：(a² - 1)/a² = ____。 31. 计算：a ÷ (a/b) = ____。

选择题 32. 下列分式中，最简分式是 ( ) A. (x² - 1)/(x + 1) B. x²y/(xy²) C. (a + b)/(a² - b²) D. 1/(x + y) 33. 若 a/b = 2/3，则 (a + b)/b 的值为 ( ) A. 2/3 B. 5/3 C. 3/2 D. 5/2

解答题 34. 计算：(1/a + 1/b) / (a + b) (解题思路：将分子通分，再进行除法运算，或转化为乘以倒数。) 35. 解分式方程：2/(x-1) = 1 + 1/x (解题思路：方程两边同乘以最简公分母 x(x-1)，转化为整式方程求解，最后要检验。)

---

参考答案与解析

第一章 三角形

1. 4 < x < 10 (根据三角形三边关系定理：两边之和大于第三边，两边之差小于第三边，7-3 < x < 7+3)
2. 65° (∠B+∠C = 180° - ∠A = 130°，因为 ∠B=∠C，∠C = 130° / 2 = 65°)
3. 50°, 50° 或 20°, 80° (分两种情况：①80°是顶角，则底角为 (180°-80°)/2 = 50°；②80°是底角，则顶角为 180°-2×80° = 20°)
4. 七 (多边形内角和公式：(n-2)·180° = 900°，解得 n = 7)
5. C (A: 2+3=5，不满足；B: 3+4<8，不满足；C: 5+6>10, 5+10>6, 6+10>5，满足；D: 4+4<9，不满足)
6. C (三角形的稳定性是其基本性质)
7. D (钝角三角形有两条高在三角形内部，一条高在三角形外部)
8. 解：在 △ABC 中，∠B = 40°，∠C = 60°， ∠BAC = 180° - ∠B - ∠C = 180° - 40° - 60° = 80°。 因为 AE 是 ∠BAC 的平分线， ∠BAE = ∠BAC / 2 = 80° / 2 = 40°。 因为 AD 是 BC 边上的高，∠ADB = 90°。 在 △ABD 中，∠BAD = 180° - ∠B - ∠ADB = 180° - 40° - 90° = 50°。 ∠DAE = ∠BAD - ∠BAE = 50° - 40° = 10°。

第二章 全等三角形

9. 40° (△ABC ≌ �DEF，∠A = ∠D = 40°，在 △DEF 中，∠F = 180° - ∠D - ∠E = 180° - 40° - 100° = 40°)
10. ∠B = ∠C (或 ∠AFB = ∠DEC，或 BF=CE)
11. D (两个锐角对应相等只能保证相似，不能保证全等)
12. D (用 HL 证明，不是 AAS，或者直接观察，SSS 是成立的，AAS 也成立，HL 也成立，只有 D 不正确)
13. 证明：因为 AB ∥ DE， ∠A = ∠D (两直线平行，内错角相等)。 因为 AF = DC， AF + FC = DC + FC， 即 AC = DF。 在 △ABC 和 △DEF 中， { ∠A = ∠D { AC = DF { AB = DE △ABC ≌ △DEF (SAS)。
14. 证明：过点 C 作 CE ⊥ BN，垂足为 E。 因为 AM ⊥ MN，BN ⊥ MN， ∠AMC = ∠CNE = 90°。 又因为 ∠ACM = ∠ECN (对顶角相等)， △AMC ≌ △CNE (AAS)。 AM = CN，MC = NE。 因为 ∠ACB = 90°，AC ⊥ BC。 又因为 BN ⊥ MN，所以四边形 BCEM 是矩形。 CE = BM。 因为 △ABC 是等腰直角三角形，AC = BC。 BM = CN。 MN = ME + NE = MC + CN = MC + BM = BC + AM。 因为 BC = AC，MN = AC + AM。 (注：此处原题结论应为 MN=BM+AN，通过证明 BM=AN，MC=CN，MN=MC+BM=AN+BM，修正一下证明思路：证明△AMC≌△CNE后，得到AM=CN，MC=NE，MN=MC+CN=MC+AM，在矩形BCEM中，BM=CE，在Rt△ABC中，AC=BC，在Rt△ACM和Rt△CEN中，∠A+∠ACM=90°，∠ECN+∠ACM=90°，A=∠ECN，又因为AC=BC=CE，所以Rt△AMC≌Rt△CNE(HL)，所以AN=BM，MN=MC+CN=AN+BM。)

第三章 轴对称

15. (-2, -3) (关于x轴对称，横坐标不变，纵坐标变为相反数)
16. 60° 或 120° (等边三角形有3条对称轴，顶角为60°；等腰三角形(非等边)有1条对称轴，顶角任意，题目说“两条”，这是有问题的，应该是“至少一条”，按常规理解，指非等边的等腰三角形，顶角可以是任意锐角或钝角，只有等边三角形有3条，等腰三角形有1条，可能是题目表述为“至少一条”，我们按“等腰三角形”理解，顶角可以是任意角度，如果题目特指“两条”，则不存在，这里我们按常见题型，理解为求顶角，答案不唯一。)
17. 13 (解析见题目)
18. D (平行四边形、矩形、菱形既是轴对称图形也是中心对称图形)
19. C (解析见题目)
20. 解：因为 △ABD 沿 AD 翻折得到 △AED， △ABD ≌ △AED。 ∠EAD = ∠BAD，∠E = ∠B。 因为 AB = AC，∠BAC = 40°， ∠B = (180° - 40°) / 2 = 70°。 ∠E = 70°，∠EAD = ∠BAD。 设 ∠BAD = x，则 ∠EAD = x。 ∠BAC = ∠BAD + ∠CAD = x + ∠CAD = 40°， ∠CAD = 40° - x。 因为 ∠ADB = 180° - ∠B - ∠BAD = 180° - 70° - x = 110° - x， ∠EDC = ∠ADB = 110° - x (对顶角相等)。 在 △AED 中，∠AED = 180° - ∠E - ∠EAD = 180° - 70° - x = 110° - x。 ∠EDC = ∠AED = 110° - x。

第四章 整式的乘除与因式分解

21. -8x⁶y³ (积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘)
22. a² - 4b² (平方差公式：(a+b)(a-b) = a² - b²)
23. x² + 4x + 4 (完全平方公式：(a+b)² = a² + 2ab + b²)
24. a(x² - 4) 或 a(x-2)(x+2) (先提公因式a，再用平方差公式分解)
25. D (A: a³·a²=a⁵；B: (a²)³=a⁶；C: (a+b)²=a²+2ab+b²)
26. B (平方差公式要求是两项平方差的形式)
27. 解：原式 = (4x² - 12xy + 9y²) - (4x² - 9y²) = 4x² - 12xy + 9y² - 4x² + 9y² = -12xy + 18y²
28. 解：原式 = (a² + 4ab + 4b²) - (a² - 4b²) = a² + 4ab + 4b² - a² + 4b² = 4ab + 8b² 当 a = 1, b = -2 时， 原式 = 4(1)(-2) + 8(-2)² = -8 + 8(4) = -8 + 32 = 24

第五章 分式

29. 1 (分母为零时，分式无意义)
30. (a-1)/a (约分，分子分母同时除以a)
31. a²/b (除以一个数等于乘它的倒数)
32. D (A: (x-1)(x+1)/(x+1) = x-1；B: x²y/xy² = x/y；C: (a+b)/(a-b)(a+b) = 1/(a-b)；D已经是最简形式)
33. B (由 a/b=2/3 得 a=2b/3，代入 (a+b)/b = (2b/3 + b)/b = (5b/3)/b = 5/3)
34. 解：原式 = ((b+a)/ab) / (a+b) = (a+b)/ab × 1/(a+b) = 1/ab
35. 解：方程两边同乘以 x(x-1)， 得 2x = x(x-1) + (x-1) 2x = x² - x + x - 1 2x = x² - 1 x² - 2x - 1 = 0 解得 x = (2 ± √(4 + 4)) / 2 = (2 ± √8) / 2 = 1 ± √2。 检验：当 x = 1+√2 或 x = 1-√2 时，x(x-1) ≠ 0。 所以原方程的解为 x = 1+√2 或 x = 1-√2。