九年级数学第二十四章核心考点有哪些？

章节概述与知识结构图

核心地位： 圆是初中几何的最后一章，它综合运用了之前学过的全等三角形、相似三角形、直角三角形、函数等知识，学好圆，不仅能解决大量几何问题,更能提升你的综合分析和逻辑推理能力。

知识结构图（思维导图）：

第二十四章 圆
│
├── 第一节 圆的基本性质
│   ├── 1. 圆的定义与相关概念（圆心、半径、直径、弦、弧、圆心角、圆周角）
│   ├── 2. 垂径定理及其推论（解决弦、弧、圆心距的问题）
│   └── 3. 圆心角、弧、弦之间的关系定理
│
├── 第二节 点和圆、直线和圆的位置关系
│   ├── 1. 点和圆的位置关系（d, r比较）
│   ├── 2. 不在同一直线上的三点确定一个圆
│   ├── 3. 三角形的外接圆与外心
│   ├── 4. 直线和圆的位置关系（d, r比较）
│   ├── 5. 切线的性质定理
│   ├── 6. 切线的判定定理
│   └── 7. 三角形的内切圆与内心
│
├── 第三节 正多边形与圆
│   ├── 1. 正多边形与圆的关系
│   ├── 2. 正多边形的计算（中心角、边长、边心距、半径）
│   └── 3. 有关圆的计算（弧长、扇形面积、圆锥的侧面积和全面积）
│
└── 第四节 弧长和扇形面积
    ├── 1. 弧长公式
    ├── 2. 扇形面积公式
    ├── 3. 圆锥的侧面积和全面积
    └── 4. 不规则图形的面积（割补法、扇形+三角形）

---

核心知识点详解

第一节 圆的基本性质

这是本章的基础,所有后续内容都建立在对这些性质的深刻理解之上。

1. 相关概念：

   • 弦： 连接圆上任意两点的线段。
   • 弧： 圆上任意两点间的部分。
   • 圆心角： 顶点在圆心的角。
   • 圆周角： 顶点在圆上,并且两边都和圆相交的角。
   • 重要关系： 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等,反之亦然。

2. 垂径定理及其推论（重点！）

   • 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
   • 模型： 直径 ⊥ 弦 ⇒ 直径平分弦、直径平分弦所对的优弧、直径平分弦所对的劣弧。
   • 推论： 平分弦（非直径）的直径垂直于弦,并且平分弦所对的两条弧。
   • 核心思想： 在圆中，只要出现“垂直”和“平分”中任意一个条件，通常可以推出另一个,这是一个非常重要的解题工具。

3. 圆周角定理（重点！）

   
   （图片来源网络，侵删）
   • 一条弧所对的圆周角等于它所对的圆心角的一半。
   • 推论1： 同弧或等弧所对的圆周角相等；同圆或等圆中,相等的圆周角所对的弧也相等。
   • 推论2（半圆定理）： 半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。
   • 核心思想： 圆周角与圆心角之间的倍数关系是解决角度计算和证明的关键。

第二节 点和圆、直线和圆的位置关系

这部分是本章的核心,也是中考命题的热点。

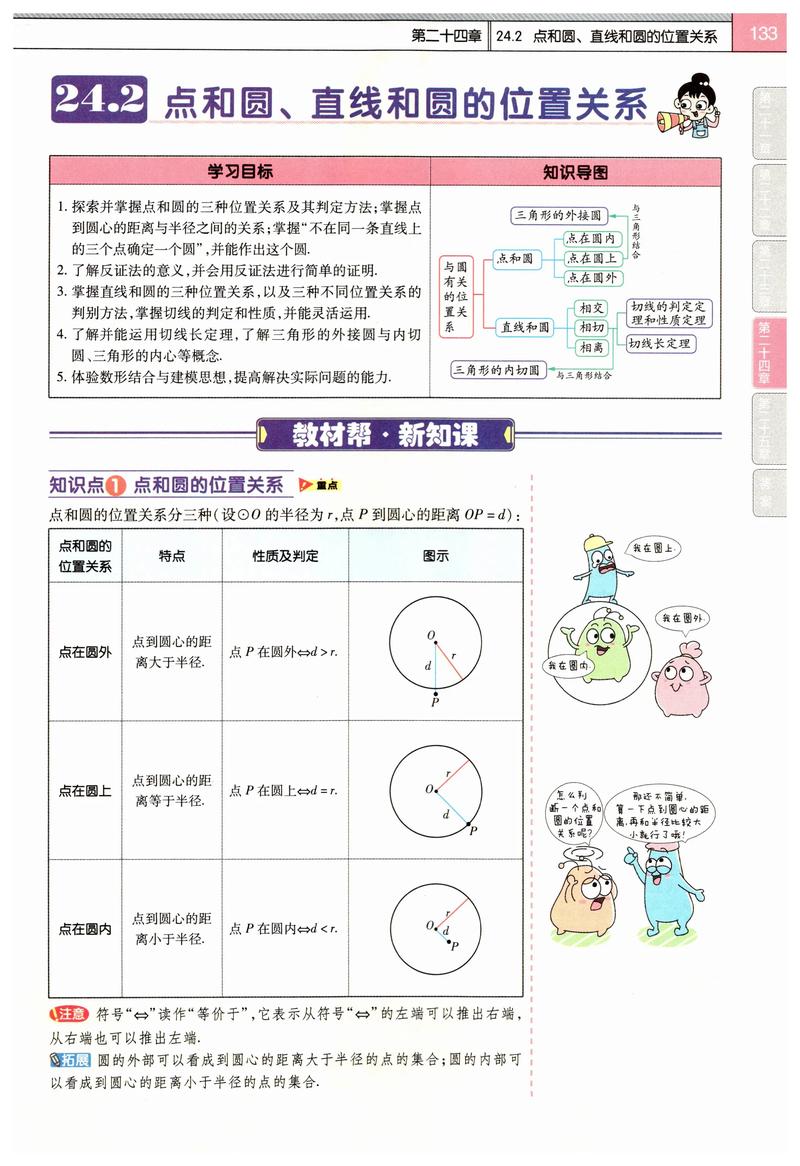
1. 点和圆的位置关系：

   • 设点到圆心的距离为 d，圆的半径为 r。
   • d < r ⇒ 点在圆内
   • d = r ⇒ 点在圆上
   • d > r ⇒ 点在圆外

2. 直线和圆的位置关系（重点！）

   • 设圆心到直线的距离为 d，圆的半径为 r。
   • d < r ⇒ 直线与圆相交（有两个公共点）
   • d = r ⇒ 直线与圆相切（有一个公共点）
   • d > r ⇒ 直线与圆相离（无公共点）
   • 核心思想： d 和 r 的关系是判断位置关系的唯一标准。

3. 切线的性质与判定（重中之重！）

   
   （图片来源网络，侵删）
   • 性质定理： 圆的切线垂直于经过切点的半径。
     • 模型： 直线是切线 + 切点 ⇒ 直线 ⊥ 半径。
   • 判定定理： 经过半径的外端并且垂直于这条半径的直线是圆的切线。
     • 模型： 直线过半径外端 + 直线 ⊥ 半径 ⇒ 直线是切线。
   • 辅助线技巧：
     • 证明直线是切线时，如果已知直线与圆有公共点（切点），则连接圆心和切点,证明垂直。
     • 如果不知道公共点，则作垂直,证明垂线段长度等于半径。

4. 三角形的“心”

   • 外接圆与外心：
     • 定义：经过三角形三个顶点的圆。
     • 外心：三角形三条边的垂直平分线的交点。
     • 性质：外心到三个顶点的距离相等。
     • 位置：锐角三角形在外部，直角三角形在斜边中点,钝角三角形在内部。
   • 内切圆与内心：
     • 定义：与三角形三条边都相切的圆。
     • 内心：三角形三个内角的角平分线的交点。
     • 性质：内心到三边的距离相等。
     • 位置：总在三角形内部。

第三节 正多边形与圆

将多边形与圆完美结合,是中考计算题的常客。

1. 关系： 任何一个正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆。
2. 核心概念：
   • 中心角 (α)： 两条相邻半径的夹角，计算公式：α = 360° / n (n为边数)。
   • 半径 (R)： 外接圆的半径。
   • 边心距 (r)： 内切圆的半径（中心到一边的距离）。
   • 边长 (a)： 正多边形的边长。
3. 计算公式： 将正多边形分割成 2n 个全等的直角三角形，这个三角形的一条直角边是边心距 r，另一条是边长的一半 a/2，斜边是半径 R,利用勾股定理和三角函数可以解决所有相关问题。

第四节 弧长和扇形面积

这部分是关于圆的“动态”计算,公式必须熟练掌握。

1. 弧长公式：

   • l = (n/360) * 2πr 或 l = (n/180) * πr
   • n 是弧所对的圆心角的度数，r 是半径。

2. 扇形面积公式：

   • S = (n/360) * πr² 或 S = (1/2)lr (l是弧长)
   • 扇形面积可以看作是圆面积的 n/360。

3. 圆锥的侧面积和全面积（重点！）

   • 展开图： 圆锥的侧面展开图是一个扇形。
   • 关系：
     • 圆锥的母线长 l = 扇形的半径。
     • 圆锥的底面周长 C = 扇形的弧长。
   • 公式：
     • 侧面积 S_侧 = (1/2) * C * l = πr * l (r 是圆锥底面半径)
     • 全面积 S_全 = S_侧 + S_底 = πr * l + πr²

---

重点、难点与易错点

• 重点：

  1. 垂径定理及其应用。
  2. 圆周角定理及其推论。
  3. 切线的性质与判定（证明题的“王牌”）。
  4. 弧长和扇形面积的计算。
  5. 圆锥侧面积和全面积的计算。

• 难点：

  1. 综合证明题： 将圆的性质、相似三角形、全等三角形、勾股定理等知识融会贯通。
  2. 动态问题： 点或直线在圆上运动,探究图形的性质或数量关系的变化。
  3. 存在性问题： 探究满足某种条件的点或直线是否存在。
  4. 不规则图形面积的计算： 需要灵活运用“割”与“补”的思想。

• 易错点：

  1. 垂径定理的使用条件： 容易忽略“直径”或“垂直”的条件,导致推理错误。
  2. 切线证明的两种情况： 混淆“连半径证垂直”和“作垂直证半径”两种方法。
  3. 圆周角定理的倍数关系： 容易把“圆周角是圆心角的一半”记反。
  4. 弧长和扇形面积公式中的 n： n 是圆心角的度数,不是弧长或面积。
  5. 圆锥计算中的 r 和 l： 容易混淆圆锥的底面半径 r 和母线长 l，以及它们与扇形半径、弧长的对应关系。

---

学习建议

1. 回归课本，夯实基础： 圆的定义、定理是解题的根本，务必把课本上的概念、定理、例题吃透,做到能自己复述和证明。
2. 动手画图，培养数形结合： 几何学习离不开图形，遇到题目，先根据题意准确画出图形,很多关系和思路在画图的过程中就会浮现。
3. 建立模型，总结方法：
   • 见到“弦”，想“垂径定理”。
   • 见到“直径”，想“90°圆周角”。
   • 见到“切线”，想“连接圆心和切点，证垂直”。
   • 见到“计算弧长/扇形面积”,想公式。
   • 见到“圆锥”,想展开图。
4. 勤加练习，重视错题： 做一定量的习题是必要的，但要更注重错题的整理和分析，建立错题本，定期回顾,确保同样的错误不再犯第二次。
5. 专题突破，攻克难关： 针对自己薄弱的环节（如存在性问题、动态问题）进行专项练习,总结解题规律和技巧。

祝你学习顺利，在圆的世界里找到乐趣，攻克难关，在中考中取得优异成绩！加油！