九年级上册数学第一次月考考什么？

校园之窗 2025年12月13日 06:26:14 99ANYc3cd6 1 0

第二十一章一元二次方程
第二十二章二次函数

这次月考非常重要，它不仅是对你开学以来学习成果的检验，更是为整个九年级数学学习打下基础的关键一战，这两章内容都是初中数学的重点和难点，并且它们之间联系紧密,常常会结合出题。

下面我为你详细梳理一下这次月考的核心考点、常见题型、备考策略和注意事项，希望能帮助你高效复习,取得好成绩！

（图片来源网络，侵删）

核心考点与知识梳理

第一章：一元二次方程

基础概念

定义：理解什么是一元二次方程（ax² + bx + c = 0，a ≠ 0）。
一般形式、顶点式、交点式：能准确识别和转换。
各项系数：能准确指出二次项系数、一次项系数和常数项。

解法（重中之重！） 你必须熟练掌握以下四种方法,并能根据方程特点选择最合适的方法：

直接开平方法：适用于 x² = a 或 (x+m)² = n 的形式。
配方法：万能方法，必须掌握！核心思想是“降次”，通过配方将方程变形为 (x+m)² = n 的形式,这是理解一元二次方程求根公式和二次函数顶点式的基础。
公式法：核心公式 x = [-b ± √(b² - 4ac)] / 2a。
- 关键：准确计算判别式 Δ = b² - 4ac。
- 判别式的作用：
  - Δ > 0 ⇔ 方程有两个不相等的实数根。
  - Δ = 0 ⇔ 方程有两个相等的实数根（一个重根）。
  - Δ < 0 ⇔ 方程没有实数根。
因式分解法：最快捷的方法，适用于能快速分解因式的方程，如 x² - 5x + 6 = 0 可分解为 (x-2)(x-3)=0。

根与系数的关系（韦达定理）

若 x₁, x₂ 是方程 ax² + bx + c = 0 的两个根，则：
- x₁ + x₂ = -b/a
- x₁ * x₂ = c/a
应用：
- 已知方程的一个根,求另一个根。
- 已知两根之和与两根之积,求一元二次方程。
- 求与方程根相关的代数式的值（如 x₁² + x₂², 1/x₁ + 1/x₂ 等）。

实际应用

（图片来源网络，侵删）

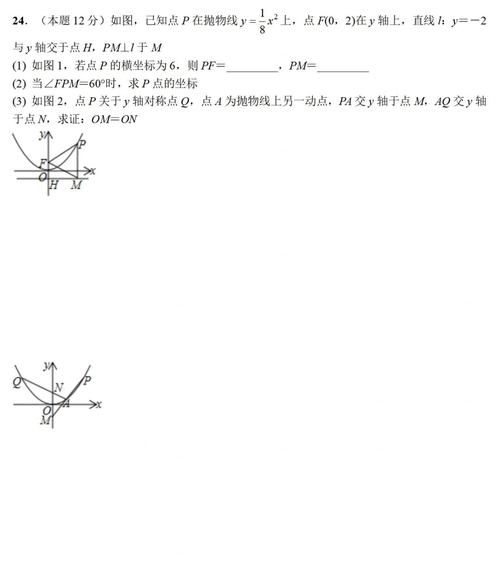
增长率/降低率问题：关键在于理解“连续两次增长/降低”的模型，如 a(1+x)² = b。
面积问题：将几何图形的面积关系转化为一元二次方程。
数字问题、营销问题等。

第二章：二次函数

基础概念

定义：理解 y = ax² + bx + c (a≠0) 是二次函数。
图像：抛物线。
系数 a, b, c 的作用：
- a：决定开口方向（a>0 向上，a<0 向下）和开口大小（|a| 越大，开口越小）。
- c：抛物线与 y 轴的交点坐标 (0, c)。
- b 和 a 共同决定对称轴的位置（对称轴 x = -b/(2a)）。

三种表达式

一般式：y = ax² + bx + c,已知图像上任意三点坐标时使用。
顶点式：y = a(x-h)² + k，已知顶点 (h, k) 和另一点坐标时使用。顶点坐标是 (h, k)，对称轴是 x = h。
交点式：y = a(x-x₁)(x-x₂)，已知抛物线与 x 轴的交点 (x₁, 0) 和 (x₂, 0) 时使用。对称轴是 x = (x₁+x₂)/2。

图像与性质

顶点坐标：(-b/(2a), (4ac-b²)/(4a)) 或 (h, k)。
对称轴：x = -b/(2a) 或 x = h。
最值：
- 当 a > 0 时，抛物线开口向上，有最小值,最小值在顶点处取得。
- 当 a < 0 时，抛物线开口向下，有最大值,最大值在顶点处取得。
与坐标轴的交点：
- 与 y 轴交点：令 x=0，求 y 值，交点为 (0, c)。
- 与 x 轴交点：令 y=0，解一元二次方程 ax² + bx + c = 0,方程的根就是交点的横坐标。

实际应用

（图片来源网络，侵删）

最值问题：利润最大化、面积最大、材料最省等，通常需要先列出二次函数关系式,然后通过求顶点坐标来解决最值问题。

常见题型与解题技巧

混合解法题：给出一个一元二次方程，让你用两种不同的方法求解。（必考！）
- 技巧：先观察方程形式，优先选择最简单的方法（如能因式分解就用因式分解，不行再配方或公式法）。
根的判别式与韦达定理综合题：
- 给出关于根的条件（如“有两个正根”、“有且只有一个根”）,求字母系数的取值范围。
- 技巧：列出关于和韦达定理的不等式（或等式）组，求解时要注意 a ≠ 0 和的条件。
二次函数图像性质分析题：
- 给出二次函数的图像或部分信息，分析 a, b, c 的符号，求顶点坐标、对称轴、与坐标轴交点等。
- 技巧：数形结合！从图像的开口方向、对称轴位置、与坐标轴交点位置等信息入手,反向推导系数的性质。
一元二次方程应用题：
- 技巧：仔细审题，找准等量关系，设未知数后，根据题意列出方程，解完方程后，一定要检验答案是否符合题意（如人数不能为负，增长率不能为负等）。
二次函数最值应用题：
- 技巧：这是难点，首先要把实际问题抽象成数学模型，即列出二次函数关系式，然后通过求顶点坐标（或配方法）来找到最值,注意自变量的取值范围。
综合探究题（压轴题雏形）：
- 将二次函数与一元二次方程、几何图形（如动点问题）结合起来。
- 技巧：这种题综合性强，需要你把各个知识点融会贯通，通常需要分步讨论，利用函数思想、方程思想、数形结合思想来解决。

备考策略与建议

回归课本，夯实基础：把课本上的定义、公式、定理重新看一遍，确保准确无误，特别是配方法和求根公式的推导过程要理解。
整理错题，查漏补缺：把开学以来的作业和练习中的错题整理到错题本上，分析错误原因：是概念不清？计算失误？还是思路不对？考前重点看错题,确保不再犯同类错误。
专题训练，突破难点：
- 解法专题：找一些一元二次方程,刻意练习用不同方法求解。
- 韦达定理专题：专门练习与根有关的代数式求值问题。
- 最值应用专题：集中练习几个典型的利润、面积最值问题。
模拟演练，适应节奏：找1-2套往年的月考卷或模拟题，在规定时间内完成，这能帮你熟悉考试题型、分值分布和时间分配,提前进入考试状态。
规范书写，减少失误：考试时，步骤要清晰，书写要规范，特别是解方程、求函数关系式时，关键步骤不能省，计算要细心,避免因粗心丢分。