七年级整式加减怎么学?关键点是什么?
校园之窗 2025年12月18日 01:00:21 99ANYc3cd6
七年级数学第二章“整式的加减”通关秘籍:从入门到精通,一篇搞定!
Meta描述: 针对七年级学生数学第二章“整式的加减”的全面学习指南,本文详细解析整式、同类项、合并同类项、去括号与添括号等核心概念,并提供独家学习技巧、典型例题和易错点分析,助你轻松攻克数学难关,期中期末考试拿高分!
引言:告别“数学恐惧症”,拿下初中数学第一座“小山丘”
亲爱的同学们,当你们翻开七年级数学课本,第二章“整式的加减”便映入眼帘,它像一座连接小学算术与初中代数的小山丘,翻过了它,你的数学思维将迎来一次质的飞跃!

很多同学初学时会觉得概念多、符号绕、计算容易出错,别担心,这非常正常!本章看似简单,实则是整个初中代数的基石,它不仅考验你的计算能力,更在培养你的逻辑思维和抽象概括能力。
作为你的教育向导,我将用最通俗易懂的语言,带你一步步拆解这座“小山丘”,从最基础的概念到最综合的应用,为你呈上一份详尽的“通关秘籍”,无论你是课前预习、课中学习,还是课后复习,这篇文章都能成为你最得力的助手。
第一关:认识“整式”——从“数”到“式”的华丽转身
在学习“加减”之前,我们首先要明白,我们到底在“加”和“减”什么,答案就是——整式。
什么是整式?
整式就是由数和字母的积组成的代数式,我们称其中的数字因数为系数,称所有字母的指数的和为次数。
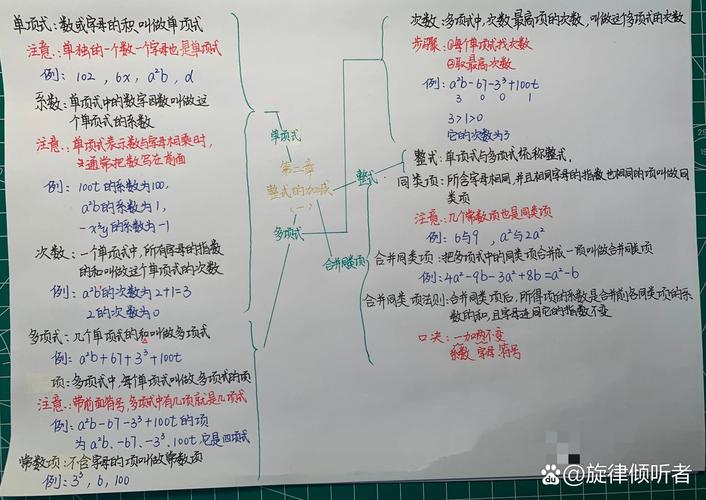
- 单项式: 像数字、单独一个字母、或字母与数字的乘积(如
5,-a,3xy²),都是单项式。3xy²的系数是3,次数是1(x的指数) +2(y的指数) =3。 - 多项式: 几个单项式的和叫做多项式。
3x² - 2x + 5就是一个二次三项式。
【学习技巧】: 想象一下,整式就像一个“大家庭”,单项式是“家庭成员”,多项式是“整个家庭”,系数是每个家庭成员的“身份标签”(前面的数字),次数则是这个家庭成员的“能力等级”(所有字母指数的总和)。
什么不是整式?
要理解什么是整式,也要知道什么不是,分母中含有字母的式子(如 1/x)和根号下含有字母的式子(如 √x),都不是整式。
第二关:合并同类项——给整式“瘦身”的核心技巧
学完了整式,我们就要进行“加减”运算了,而运算的第一步,也是最重要的一步,就是合并同类项。
什么是同类项?
同类项,顾名思义,长得像”的项,判断两个项是不是同类项,有两大黄金法则:

- 所含字母完全相同。
- 相同字母的指数也相同。
特别注意:
- 常数项都是同类项。
5和-100。 - 系数不同没关系,字母的顺序没关系。
3ab和-7ba是同类项。
【易错点警示】:
很多同学会误认为 3x²y 和 3xy² 是同类项,相同字母的指数也必须相同!这里的 x 和 y 的指数位置互换了,所以不是。
如何合并同类项?
合并同类项的法则是:系数相加,字母和字母的指数不变。
公式:axⁿ + bxⁿ = (a+b)xⁿ
【经典例题】
合并下列多项式中的同类项:
4a²b - 3ab² + 1/2a²b + 6ab² - 5
【解题步骤】
- 标记同类项:用不同的符号或线标出同类项。
(4a²b + 1/2a²b) + (-3ab² + 6ab²) - 5 - 合并系数:
a²b的系数:4 + 1/2 = 9/2ab²的系数:-3 + 6 = 3- 常数项:
-5
- 写出结果:
(9/2)a²b + 3ab² - 5
【学习技巧】:
合并同类项就像超市购物结账,把所有苹果(a²b)放在一起算总价,所有香蕉(ab²)放在一起算总价,最后再把总价加起来,这样是不是就清晰多了?
第三关:去括号与添括号——符号运用的“魔术”
合并同类项之后,我们常常会遇到带括号的多项式,这时,就需要掌握去括号和添括号的技巧了。
去括号法则
去括号,本质是乘法分配律的应用,记住口诀:“括号前面是正号,去掉括号不变号;括号前面是负号,去掉括号全变号。”
+(a+b-c) = a+b-c-(a+b-c) = -a-b+c
【易错点警示】: 最容易出错的就是括号前面是负号的情况,同学们一定要记住,括号里的每一项都要变号,不能只变第一项!
【经典例题】
化简:3a - 2(a - b) + (a + b)
【解题步骤】
- 去括号:
3a - 2a + 2b + a + b(注意:-2乘以括号里的-b得+2b)
- 合并同类项:
(3a - 2a + a) + (2b + b)2a + 3b
添括号法则
添括号是去括号的逆运算,法则与之类似:
- 括号前面是正号,括到括号里的各项符号不变。
- 括号前面是负号,括到括号里的各项符号全变。
【应用场景】: 添括号通常用于因式分解或改变多项式的某一部分符号,在整式加减中相对较少,但理解它有助于你更深刻地掌握去括号。
第四关:整式的加减——综合运算大挑战
掌握了以上所有技巧,我们就可以进行整式的加减混合运算了,其核心思想是:先去括号,再合并同类项。
【综合例题】
求 3x²y - [2xy² - 4(x²y - xy²) - x²y] 的值,x=1, y=-2。
【解题步骤】
- 从内到外去括号:
- 先处理最里面的小括号:
4(x²y - xy²) = 4x²y - 4xy² - 原式变为:
3x²y - [2xy² - (4x²y - 4xy²) - x²y] - 接着处理中括号里的负号:
-(4x²y - 4xy²) = -4x²y + 4xy² - 原式变为:
3x²y - [2xy² - 4x²y + 4xy² - x²y]
- 先处理最里面的小括号:
- 合并中括号内的同类项:
2xy² + 4xy² = 6xy²-4x²y - x²y = -5x²y- 中括号内变为:
6xy² - 5x²y - 原式变为:
3x²y - (6xy² - 5x²y)
- 去最后的括号:
3x²y - 6xy² + 5x²y
- 合并最终的同类项:
3x²y + 5x²y = 8x²y- 结果为:
8x²y - 6xy²
- 代入数值求值:
8(1)²(-2) - 6(1)(-2)²8 * 1 * (-2) - 6 * 1 * 4-16 - 24 = -40
【学习技巧】: 做这种复杂运算时,一定要耐心细致,一步一步来,建议在草稿纸上清晰地写出每一步的去括号过程,避免眼高手低导致符号错误。
第五关:本章知识体系与学习策略
为了让你对全章有更宏观的把握,这里为你梳理知识体系图:
整式的加减
|
+----------------+-----------------+
| |
整式的概念 整式的运算
| |
+-------+-------+ +---------+---------+
| | | |
单项式 (系数,次数) 多项式 (项,次数) 合并同类项 去括号与添括号
| | | (系数相加) (符号法则)
+-------+-------+ +---------+---------+
| |
+----------------+-----------------+
|
综合化简与求值【高效学习策略】:
- 理解优先,记忆在后:不要死记硬背法则,要理解其背后的数学原理(如乘法分配律)。
- 错题本是你的宝藏:准备一个错题本,把所有做错的题目抄下来,旁边写下正确解法和错误原因,考前翻一翻,效果奇佳。
- 勤于练习,熟能生巧:数学是“做”出来的,不是“看”出来的,每天做几道不同类型的题目,保持手感。
- 敢于提问,不留死角:有任何疑问,立刻请教老师或同学,不要把问题堆积起来。
打好地基,盖起数学的“摩天大楼”
同学们,“整式的加减”这一章,就像我们初中代数大厦的“地基”,它看似简单,却承载着未来学习一元一次方程、整式乘除、因式分解乃至函数的巨大重量。
希望这份“通关秘籍”能帮助你拨开迷雾,找到学习的乐趣和方向,数学的世界充满了逻辑与美感,只要你一步一个脚印,耐心探索,就一定能领略到它的魅力,就带着这份自信,去征服你的“小山丘”吧!
互动话题:你在学习“整式的加减”时,遇到过哪些难题?或者有什么独家的学习小技巧?欢迎在评论区留言分享,我们一起交流进步!



