六年级圆的练习题有哪些典型考点？

第一部分：基础题 (巩固概念和公式)

这部分主要考察圆的基本概念、周长和面积公式的直接应用。

填空题

1. 在同一个圆或等圆中，有（ ）条半径，有（ ）条直径，直径的长度是半径的（ ）倍，半径的长度是直径的（ ）。
2. 圆周率π是一个（ ）小数，它约等于（ ）。
3. 一个圆的半径是4厘米，它的直径是（ ）厘米，周长是（ ）厘米，面积是（ ）平方厘米。
4. 一个圆形花坛的周长是18.84米，它的半径是（ ）米。
5. 用一根绳子刚好可以围成一个半径是3分米的圆，如果用这根绳子去围一个正方形，这个正方形的边长是（ ）分米。
6. 一个圆形铁片的半径扩大到原来的2倍，它的直径扩大到原来的（ ）倍，周长扩大到原来的（ ）倍，面积扩大到原来的（ ）倍。

判断题 (对的打“√”，错的打“×”)

1. 直径是圆内最长的线段。 （ ）
2. 两个圆的周长相等，那么它们的面积也一定相等。 （ ）
3. 半径是2厘米的圆，它的周长和面积相等。 （ ）
4. π等于3.14。 （ ）
5. 一个圆的半径增加1厘米，它的直径也增加1厘米。 （ ）

选择题 (将正确答案的序号填在括号里)

1. 一个圆的周长是15.7厘米，它的直径是（ ）。 A. 5厘米 B. 10厘米 C. 2.5厘米

2. 一个圆形桌面，直径是1米，它的面积是（ ）。 A. 3.14平方米 B. 6.28平方米 C. 78.5平方米

   
   （图片来源网络，侵删）

3. 一个圆形纸片，半径从3厘米增加到5厘米，面积增加了（ ）平方厘米。 A. 2 B. 16 C. 50.24

4. 要给一个直径是10米的圆形喷水池围上栅栏，栅栏的长至少是（ ）。 A. 31.4米 B. 78.5米 C. 314米

---

第二部分：提高题 (综合运用与巧算)

需要综合运用周长和面积公式,或者通过巧妙的分析来解决问题。

1. 一个半圆形的周长是20.56厘米，求这个半圆的面积。（提示：半圆的周长 = πr + 2r）
2. 一个圆形运动场，跑道周长是400米，这个运动场的直径大约是多少米？（结果保留整数）
3. 一个长方形的纸片，长10厘米，宽8厘米，在这个纸片上剪下一个最大的圆,这个圆的周长和面积各是多少？
4. 一个圆形和一个正方形的周长相等，已知正方形的边长是6.28分米,那么圆形的面积是多少平方分米？
5. 一个圆环，外圆半径是8厘米，内圆半径是5厘米，求这个圆环的面积。（提示：圆环面积 = π(R² - r²)）

---

第三部分：应用题 (解决生活中的问题)

将圆的知识与生活实际相结合,考验你的读题和建模能力。

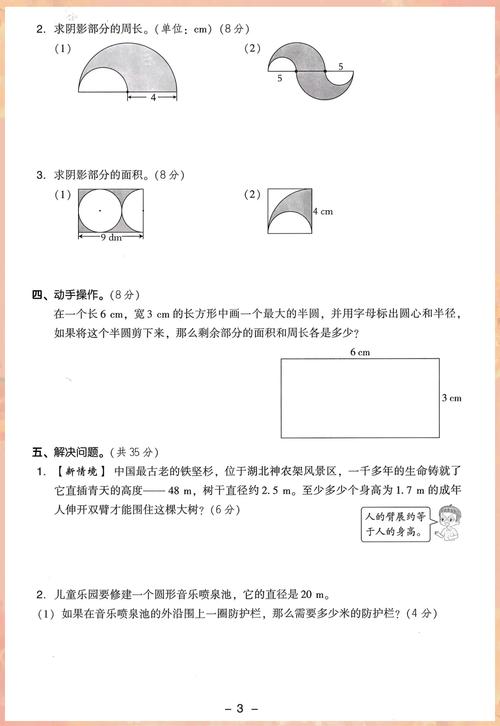
1. 一个圆形喷水池的半径是8米，在它的周围修一条宽1米的环形小路。 (1) 这条小路的面积是多少平方米？ (2) 如果沿着小路的外边缘每隔4米装一盏灯,大约需要装多少盏灯？

2. 一个圆形牛栏的半径是12米，李爷爷用一根长25米的绳子把牛拴在牛栏边的一个木桩上,牛能吃到草的最大面积是多少平方米？

3. 一个圆形花坛的直径是10米，在它的周围修一条宽2米的环形小路。 (1) 这个花坛的占地面积是多少平方米？ (2) 这条小路的面积是多少平方米？ (3) 如果给小路铺上每平方米20元的地砖,需要多少钱？

4. 一个圆形钟面的直径是20厘米，钟面的面积是多少平方厘米？如果时针的长度是10厘米，时针尖端一昼夜（24小时）走过的路程是多少厘米？

---

参考答案与解析

第一部分：基础题

填空题

1. 无数，无数，2，1/2。
2. 无限不循环，3.14。
3. 直径：4 × 2 = 8厘米；周长：3.14 × 8 = 25.12厘米；面积：3.14 × 4² = 3.14 × 16 = 50.24平方厘米。
4. 周长 = 2πr，r = 周长 ÷ (2π) = 18.84 ÷ (2 × 3.14) = 18.84 ÷ 6.28 = 3米。
5. 绳子长 = 圆的周长 = 2πr = 2 × 3.14 × 3 = 18.84分米，围成正方形，边长 = 18.84 ÷ 4 = 4.71分米。
6. 2倍，2倍，4倍。（面积与半径的平方成正比）

判断题

1. √ （直径是圆内通过圆心最长的线段）
2. √ （周长相等意味着半径相等,半径相等的圆面积也相等）
3. × （周长和面积的单位不同,数值上不可能相等）
4. × （π是无限不循环小数，3.14是它的近似值）
5. × （直径是半径的2倍，半径增加1厘米,直径应增加2厘米）

选择题

1. A （d = C ÷ π = 15.7 ÷ 3.14 = 5厘米）
2. A （r = d ÷ 2 = 1 ÷ 2 = 0.5米，S = πr² = 3.14 × 0.5² = 0.785平方米，选项A是πr²,是正确答案）
3. C （原面积 S₁ = π × 3² = 9π；新面积 S₂ = π × 5² = 25π；增加的面积 = 25π - 9π = 16π ≈ 16 × 3.14 = 50.24平方厘米）
4. A （栅栏的长度就是圆的周长，C = πd = 3.14 × 10 = 31.4米）

第二部分：提高题

1. 解： 设半圆的半径为r。 半圆周长 = πr + 2r = 20.56 3.14r + 2r = 20.56 5.14r = 20.56 r = 20.56 ÷ 5.14 = 4 (厘米) 半圆面积 = (πr²) ÷ 2 = (3.14 × 4²) ÷ 2 = (3.14 × 16) ÷ 2 = 25.12 (平方厘米)

2. 解： 跑道周长就是圆形的周长，C = 400米。 d = C ÷ π = 400 ÷ 3.14 ≈ 127.39 (米) 答：这个运动场的直径大约是127米。

3. 解： 在长方形纸片上剪下的最大圆，其直径等于长方形的宽，即8厘米。 半径 r = 8 ÷ 2 = 4 (厘米) 圆的周长 C = 2πr = 2 × 3.14 × 4 = 25.12 (厘米) 圆的面积 S = πr² = 3.14 × 4² = 50.24 (平方厘米)

4. 解： 正方形周长 = 4 × 边长 = 4 × 6.28 = 25.12 (分米) 因为圆形和正方形周长相等，所以圆形周长C = 25.12分米。 圆的半径 r = C ÷ (2π) = 25.12 ÷ (2 × 3.14) = 25.12 ÷ 6.28 = 4 (分米) 圆的面积 S = πr² = 3.14 × 4² = 50.24 (平方分米)

5. 解： R = 8厘米，r = 5厘米。 圆环面积 = π(R² - r²) = 3.14 × (8² - 5²) = 3.14 × (64 - 25) = 3.14 × 39 = 122.46 (平方厘米)

第三部分：应用题

1. 解： (1) 外圆半径 R = 8 + 1 = 9 (米) 小路面积 = 外圆面积 - 内圆面积 = π(R² - r²) = 3.14 × (9² - 8²) = 3.14 × (81 - 64) = 3.14 × 17 = 53.38 (平方米) (2) 外圆周长 C = 2πR = 2 × 3.14 × 9 = 56.52 (米) 需要装灯的数量 = 56.52 ÷ 4 ≈ 14.13 (盏) 答：大约需要装14盏灯。

2. 解： 牛能吃到草的最大范围是以木桩为圆心，绳子长为半径的圆。 半径 r = 绳长 = 25米。 最大面积 S = πr² = 3.14 × 25² = 3.14 × 625 = 1962.5 (平方米) 答：牛能吃到草的最大面积是1962.5平方米。

3. 解： (1) 花坛半径 r = 10 ÷ 2 = 5 (米) 花坛面积 S₁ = πr² = 3.14 × 5² = 78.5 (平方米) (2) 外圆半径 R = 5 + 2 = 7 (米) 小路面积 = 外圆面积 - 花坛面积 = π(R² - r²) = 3.14 × (7² - 5²) = 3.14 × (49 - 25) = 3.14 × 24 = 75.36 (平方米) (3) 铺地砖总价 = 小路面积 × 单价 = 75.36 × 20 = 1507.2 (元) 答：需要1507.2元。

4. 解： (1) 钟面半径 r = 20 ÷ 2 = 10 (厘米) 钟面面积 S = πr² = 3.14 × 10² = 314 (平方厘米) (2) 时针长度就是它的半径，r = 10厘米。 时针12小时转一圈，24小时转两圈。 时针尖端走过的路程相当于两个圆的周长。 C = 2πr = 2 × 3.14 × 10 = 62.8 (厘米) 总路程 = 62.8 × 2 = 125.6 (厘米) 答：时针尖端一昼夜走过的路程是125.6厘米。

希望这些练习题对你有帮助！如果还有不懂的地方,随时可以再提问。