2025年希望杯八年级试题难度如何？

校园之窗 2025年12月17日 04:51:16 99ANYc3cd6 1 0

2025年希望杯八年级部分真题回忆及解析

以下是根据网络资源整理的部分典型题目,并附上详细的解析，希望能帮助您了解其风格和难度。

选择题

第1题 (约等于考察估算和数感) 计算：$\sqrt{2025^2 - 4028 + 4}$ 的值是（） A. 2010 B. 2012 C. 2025 D. 2025

（图片来源网络，侵删）

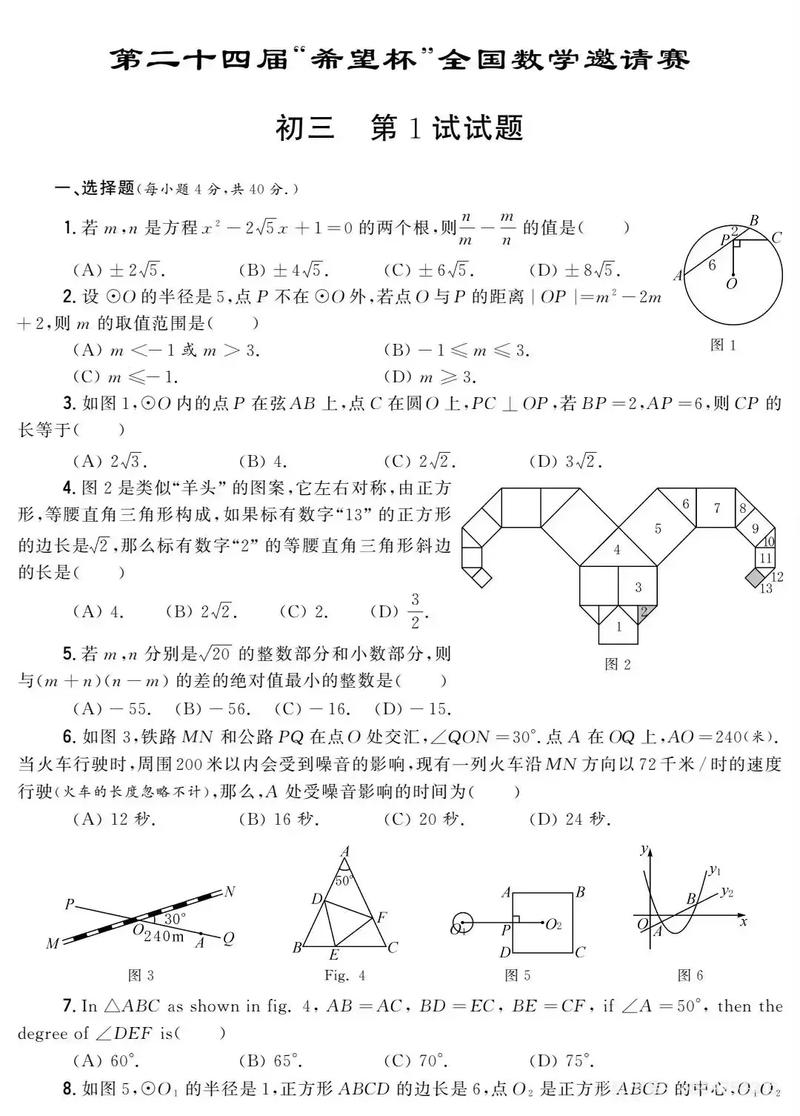
【解析】 这道题考察的是完全平方公式的应用。 $\sqrt{2025^2 - 4028 + 4} = \sqrt{2025^2 - 2 \times 2025 \times 2 + 2^2}$ 观察根号内的部分，它符合完全平方公式 $a^2 - 2ab + b^2 = (a-b)^2$ 的形式。这里 $a=2025$, $b=2$。原式 $= \sqrt{(2025 - 2)^2} = \sqrt{2012^2} = 2012$。 答案：B

第2题 (约等于考察几何图形性质) 如图，在平行四边形 $ABCD$ 中，$E$ 是边 $AD$ 的中点，$BE$ 交对角线 $AC$ 于点 $F$，则 $AF:FC$ 的值为（） A. 1:1 B. 1:2 C. 1:3 D. 2:3

【解析】 这道题是平行四边形和相似三角形的经典模型。 利用相似三角形 在 $\triangle AEF$ 和 $\triangle CDF$ 中： $\angle EAF = \angle FCG$ (对顶角相等) $\angle AEF = \angle CFD$ (内错角相等，因为 $AD \parallel BC$) $\triangle AEF \sim \triangle CDF$ (AA相似)。因为 $E$ 是 $AD$ 的中点，$AE:CD = 1:2$。相似比 $k=1:2$，对应边成比例，$AF:FC = 1:2$。

利用面积法 (更巧妙) 连接 $BD$，交 $AC$ 于点 $O$，在平行四边形中，对角线互相平分，$O$ 是 $AC$ 的中点，即 $AO=OC$。连接 $OE$，因为 $E$ 是 $AD$ 的中点，$O$ 是 $BD$ 的中点，$OE$ 是 $\triangle ABD$ 的中位线，$OE \parallel AB$ 且 $OE = \frac{1}{2}AB$。因为 $OE \parallel AB$，$\triangle EOF \sim \triangle ABF$。相似比 $k = OE:AB = 1:2$。 $OF:BF = 1:2$。设 $OF=x$，则 $BF=2x$，$BO = BF+OF = 3x$。又因为 $O$ 是 $BD$ 的中点，$BD = 2BO = 6x$。 $OD = BO = 3x$。现在看 $\triangle ABD$，$E$ 是中点，$F$ 在 $BD$ 上。根据梅涅劳斯定理或直接观察，$\frac{AF}{FC} = \frac{AE}{ED} \cdot \frac{DO}{OB}$，因为 $AE=ED$, $DO=OB$，所以这个方法在这里不直接适用。我们回到面积比。$\triangle ABO$ 和 $\triangle CBO$ 面积相等（等底同高）。$\triangle AFO$ 和 $\triangle CFO$ 面积也相等（等底同高）。$\triangle ABF$ 和 $\triangle CBF$ 面积相等。 $S{\triangle ABF} = S{\triangle CBF}$。 $S{\triangle ABF} = S{\triangle AOF} + S{\triangle AOB}$ $S{\triangle CBF} = S{\triangle COF} + S{\triangle COB}$ 因为 $S{\triangle AOF} = S{\triangle COF}$ 且 $S{\triangle AOB} = S{\triangle COB}$，所以这个等式成立，但没有直接给出比例。我们使用方法一更直接。 答案：B

（图片来源网络，侵删）

希望杯八年级考察重点分析

可以看出,2025年希望杯八年级的考察重点主要集中在以下几个方面：

代数基础：
- 实数与运算：绝对值、算术根、幂的运算，选择题第1题就是典型代表。
- 代数式：整式、分式的化简与求值，因式分解，特别是完全平方、平方差公式的灵活运用。
- 方程与不等式：一元一次、一元二次方程的解法与应用，分式方程，含参数的方程与不等式，以及方程组的解法。
- 函数：一次函数、反比例函数的图像与性质，重点是结合几何图形解决动点问题、面积问题等。
几何核心：
- 三角形：全等与相似的判定与性质是重中之重，选择题第2题就是相似三角形的经典应用，还会考察角平分线、中线、高线的性质，以及勾股定理及其逆定理。
- 四边形：平行四边形、矩形、菱形、正方形的性质与判定，特别是对角线的性质，梯形的性质也会涉及。
- 圆：垂径定理、圆周角定理、圆心角定理、切线的性质与判定等，这是几何部分的难点和重点。
数学思想与方法：
（图片来源网络，侵删）
- 数形结合思想：将代数问题（如函数、不等式）与几何图形（如坐标系、线段）相结合，是希望杯的核心思想。
- 分类讨论思想：在解决含绝对值、含参数、动点等问题时，需要根据不同情况进行讨论。
- 转化与化归思想：将复杂问题转化为简单问题，将未知问题转化为已知问题（如将比例问题转化为相似三角形问题）。
- 整体思想：在代数式化简中，把一个式子看作一个整体进行处理。

备考建议

希望杯的备考不应只盯着难题,而应注重基础和思维的培养。

回归课本，夯实基础：确保课本上的基本概念、公式、定理烂熟于心，这是解决一切问题的前提。
专题训练，突破难点：
- 代数：重点练习代数式的恒等变形、复杂方程（组）的解法、函数与几何的综合题。
- 几何：系统梳理全等与相似的证明方法，熟练掌握各种基本模型（如“A”型、“X”型、“母子”型等），多练习动态几何问题。
研究真题，把握风格：做近几年的希望杯真题，感受其命题风格、难度和常见的“陷阱”，分析错题，总结解题思路。
培养数学思维：在解题时，多问自己“为什么这么做？”“还有别的方法吗？”，尝试一题多解，培养发散性思维，学会归纳总结，将同类型的题目和解法归类整理。
模拟训练，提升速度：在备考后期，进行限时模拟训练，合理分配时间，提高解题速度和准确率。