九年级上册数学知识点有哪些?
校园之窗 2025年12月15日 10:45:35 99ANYc3cd6
九年级上册数学(人教版)核心知识总结
九年级上册数学是整个初中数学的“重头戏”,内容多、难度大,且与后续学习(尤其是高中数学)紧密相连,核心内容可以概括为:一元二次方程、二次函数、圆、以及概率初步。
第一章 一元二次方程
核心地位: 这是初中代数的核心内容之一,是解决实际问题的有力工具,也是后续学习二次函数的基础。

知识结构
-
基本概念
- 定义: 只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程,叫做一元二次方程。
- 一般形式:
ax² + bx + c = 0(a, b, c是常数,且 a ≠ 0)a是二次项系数,b是一次项系数,c是常数项。
- 识别关键: 必须是整式方程,且最高次数为2,
a绝对不能为0。
-
解法(降次思想)
- 直接开平方法: 形如
(x + m)² = n(n ≥ 0) 的方程。- 思路: 直接对
x + m开平方,得到x + m = ±√n。 - 适用: 适合方程左边是完全平方式,右边是非负数的情况。
- 思路: 直接对
- 配方法
- 核心思想: 将方程
ax² + bx + c = 0转化为(x + m)² = n的形式。 - 步骤:
- 二次项系数化为1:
x² + (b/a)x + c/a = 0。 - 移项:
x² + (b/a)x = -c/a。 - 配方:方程两边同时加上一次项系数一半的平方,即
(b/2a)²。 - 化为完全平方式:
[x + (b/2a)]² = (b² - 4ac)/(4a²)。 - 用直接开平方法求解。
- 二次项系数化为1:
- 意义: 推导求根公式的基础,也是研究二次函数顶点式的重要方法。
- 核心思想: 将方程
- 公式法
- 求根公式:
x = [-b ± √(b² - 4ac)] / (2a)(a ≠ 0) - 使用前提: 必须先将方程化为一般形式
ax² + bx + c = 0。 - 关键: 计算判别式 (Δ)。
- 判别式 (Δ):
Δ = b² - 4ac - Δ的作用:
Δ > 0⇒ 方程有两个不相等的实数根。Δ = 0⇒ 方程有两个相等的实数根(或说有一个重根)。Δ < 0⇒ 方程没有实数根。
- 判别式 (Δ):
- 求根公式:
- 因式分解法
- 核心思想: 将方程左边化为两个一次因式的乘积,右边为0,再利用“若 A·B = 0,则 A=0 或 B=0”求解。
- 常用方法: 提公因式法、公式法(平方差、完全平方)、十字相乘法。
- 优点: 当方程易于因式分解时,此法最简便快捷。
- 直接开平方法: 形如
-
根与系数的关系(韦达定理)
- 若一元二次方程
ax² + bx + c = 0(a ≠ 0) 的两个根为x₁和x₂,则:x₁ + x₂ = -b/ax₁ · x₂ = c/a
- 应用:
- 已知方程的一根,求另一根。
- 已知两根的和与积,求作一元二次方程。
- 不解方程,求与方程根相关的代数式的值(如
x₁² + x₂²,1/x₁ + 1/x₂等)。
- 若一元二次方程
-
实际应用
 (图片来源网络,侵删)
(图片来源网络,侵删)- 题型: 增长率问题、利润问题、面积问题、数字问题等。
- 关键步骤:
- 审题: 找出等量关系。
- 设元: 合理设未知数。
- 列方程: 根据等量关系列出方程。
- 解方程: 选择合适的方法求解。
- 检验作答: 检验解是否符合题意(如人数、时间不能为负数)。
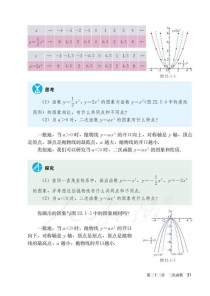
第二章 二次函数
核心地位: 这是初中数学的又一个重点和难点,是函数学习的巅峰,其图像和性质完美体现“数形结合”思想,是高中学习更复杂函数的基础。
知识结构
-
基本概念
- 定义: 形如
y = ax² + bx + c(a, b, c是常数,且 a ≠ 0) 的函数,叫做二次函数。 - 自变量:
x,取值范围是全体实数。
- 定义: 形如
-
图像与性质
- 图像: 抛物线。
- 解析式形式:
- 一般式:
y = ax² + bx + c(a ≠ 0)便于研究函数的对称轴、顶点坐标。
 (图片来源网络,侵删)
(图片来源网络,侵删) - 顶点式:
y = a(x - h)² + k(a ≠ 0)(h, k)是抛物线的顶点坐标。x = h是抛物线的对称轴。a决定开口方向和大小。
- 交点式(双根式):
y = a(x - x₁)(x - x₂)(a ≠ 0)x₁,x₂是抛物线与 x 轴交点的横坐标。- 对称轴为
x = (x₁ + x₂) / 2。
- 一般式:
- 性质(以
y = ax² + bx + c为例): | 性质 | a > 0 | a < 0 | | :--- | :--- | :--- | | 开口方向 | 向上 | 向下 | | 顶点坐标 |(-b/(2a), (4ac-b²)/(4a))|(-b/(2a), (4ac-b²)/(4a))| | 对称轴 |x = -b/(2a)|x = -b/(2a)| | 增减性 | x > -b/(2a)时,y随x增大而增大;x < -b/(2a)时,y随x增大而减小。 | x > -b/(2a)时,y随x增大而减小;x < -b/(2a)时,y随x增大而增大。 | | 最值 | 有最小值,y_min = (4ac-b²)/(4a) | 有最大值,y_max = (4ac-b²)/(4a) |
-
二次函数与一元二次方程、不等式的关系(数形结合)
- 交点: 抛物线
y = ax² + bx + c与 x 轴的交点横坐标,就是方程ax² + bx + c = 0的根。 - 位置关系(由判别式Δ决定):
Δ > 0⇒ 抛物线与 x 轴有两个交点。Δ = 0⇒ 抛物线与 x 轴有一个交点(顶点在x轴上)。Δ < 0⇒ 抛物线与 x 轴没有交点。
- 不等式:
ax² + bx + c > 0的解集,对应抛物线在 x 轴上方的部分。ax² + bx + c < 0的解集,对应抛物线在 x 轴下方的部分。
- 交点: 抛物线
-
实际应用
- 最优化问题: 求最大利润、最大面积、最高点、最远距离等。
- 方法: 建立二次函数模型,通过求其最大值或最小值来解决。
第三章 旋转
核心地位: 本章是图形变换的重要组成部分,与全等、相似、圆等几何知识联系紧密,是培养空间观念和逻辑推理能力的关键章节。
知识结构
-
旋转的定义
- 要素: 旋转中心、旋转方向、旋转角度。
- 性质:
- 对应点到旋转中心的距离相等。
- 对应点与旋转中心所连线段的夹角等于旋转角。
- 旋转前后的两个图形全等。
-
中心对称
- 定义: 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点中心对称,这个点叫做对称中心。
- 性质:
- 关于中心对称的两个图形是全等图形。
- 对称点连线都经过对称中心,并且被对称中心平分。
- 中心对称图形: 一个图形绕某个点旋转180°后,如果能够与原图形重合,那么这个图形就是中心对称图形。
- 常见图形: 平行四边形、矩形、菱形、正方形、圆等。
第四章 圆
核心地位: 平面几何的集大成者,内容多、定理多、综合性强,是中考压轴题的常客。
知识结构
-
圆的基本概念
定义、弦、直径、弧、半圆、优弧、劣弧、等弧、圆心角、圆周角、弦心距。
-
垂径定理及其推论
- 定理: 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
- 推论: 平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧。
- 核心: 知二推三(已知垂直、平分弦、平分优弧、平分劣弧这五个条件中的任意两个,都可以推出另外三个)。
-
圆心角、弧、弦之间的关系
- 定理: 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
- 推论: 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
-
圆周角定理
- 定理: 一条弧所对的圆周角等于它所对的圆心角的一半。
- 推论1: 同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等。
- 推论2: 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
-
点和圆的位置关系
- 设圆心到点的距离为
d,半径为r。d < r⇒ 点在圆内。d = r⇒ 点在圆上。d > r⇒ 点在圆外。
- 设圆心到点的距离为
-
直线和圆的位置关系
- 设圆心到直线的距离为
d,半径为r。d < r⇒ 直线与圆相交(有两个交点)。d = r⇒ 直线与圆相切(有一个交点,即切点)。d > r⇒ 直线与圆相离(无交点)。
- 切线的性质与判定
- 性质: 圆的切线垂直于经过切点的半径。
- 判定: 经过半径的外端并且垂直于这条半径的直线是圆的切线。
- 设圆心到直线的距离为
-
三角形的外接圆与内切圆
- 外接圆: 经过三角形三个顶点的圆,圆心是三角形三条边的垂直平分线的交点,叫做外心。
- 内切圆: 与三角形三边都相切的圆,圆心是三角形三个内角的角平分线的交点,叫做内心。
-
正多边形与圆
- 任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆。
- 计算正多边形的边长、周长、面积等,通常将其分割成若干个全等的等腰三角形。
第五章 概率初步
核心地位: 从确定性数学过渡到随机性数学的桥梁,是理解数据统计的基础。
知识结构
-
基本概念
- 必然事件: 在一定条件下必然会发生的事件 (P=1)。
- 不可能事件: 在一定条件下必然不会发生的事件 (P=0)。
- 随机事件: 在一定条件下可能发生也可能不发生的事件 (0 < P < 1)。
-
概率的意义
- 概率是刻画随机事件发生可能性大小的数值。
- 对于一个随机事件,发生的机会越大,其概率越接近1;发生的机会越小,其概率越接近0。
-
概率的计算方法
- 列举法(适用于所有可能结果有限且等可能的情况)
- 列表法: 当涉及两个因素时,用表格列出所有可能的结果。
- 画树状图法: 当涉及三个或更多因素时,用树状图列出所有可能的结果。
- 公式法:
P(事件A) = (事件A所包含的可能结果数) / (所有可能结果的总数)
- 列举法(适用于所有可能结果有限且等可能的情况)
-
用频率估计概率
- 当试验的所有可能结果不是等可能的,或难以用列举法计算时,可以通过大量重复试验,用事件发生的频率来估计概率。
- 规律: 当试验次数足够大时,事件发生的频率会稳定在某个常数附近,这个常数就是该事件的概率。
期末复习建议
- 回归课本,夯实基础: 重新阅读课本的定义、定理、公式,确保准确无误。
- 梳理知识,构建网络: 使用思维导图等工具,将各章节的知识点串联起来,形成知识体系。
- 重视错题,查漏补缺: 整理平时的作业和考试中的错题,分析错误原因,确保不再犯同类错误。
- 专题训练,突破难点: 针对二次函数、圆等综合性强的章节,进行专题练习,掌握常见解题模型和技巧。
- 模拟演练,提升能力: 在复习后期,进行限时模拟考试,培养时间分配能力和应试心态。
祝你学习进步,期末取得优异成绩!