北师八上数学知识点有哪些重点难点？

北师大版八年级上册数学知识点总结

八年级上册的数学内容是初中阶段承上启下的关键,难度和深度都有所增加，特别是几何证明和函数思想的引入，是学习的重点和难点。

---

第一章 勾股定理

本章是几何学的第一个重要定理,揭示了直角三角形三边之间的数量关系。

核心知识点：

1. 勾股定理:

   • 如果直角三角形的两条直角边长分别为 a，b，斜边长为 c，a² + b² = c²。
   • 作用： 已知直角三角形的两边，求第三边。
   • 前提： 必须在直角三角形中才成立。

2. 勾股定理的逆定理:

   • 如果三角形的三边长 a，b，c 满足 a² + b² = c²，那么这个三角形是直角三角形。
   • 作用： 判断一个三角形是否为直角三角形。
   • 勾股数： 能满足 a² + b² = c² 的三个正整数 a，b，c 称为勾股数，3, 4, 5；5, 12, 13；6, 8, 10 等。

重点与难点：

• 重点： 勾股定理及其逆定理的理解和应用。
• 难点：
  • 在复杂的图形中构造直角三角形来应用勾股定理。
  • 利用勾股定理解决实际问题（如最短路径问题）。
  • 灵活运用勾股定理的逆定理进行证明和判断。

---

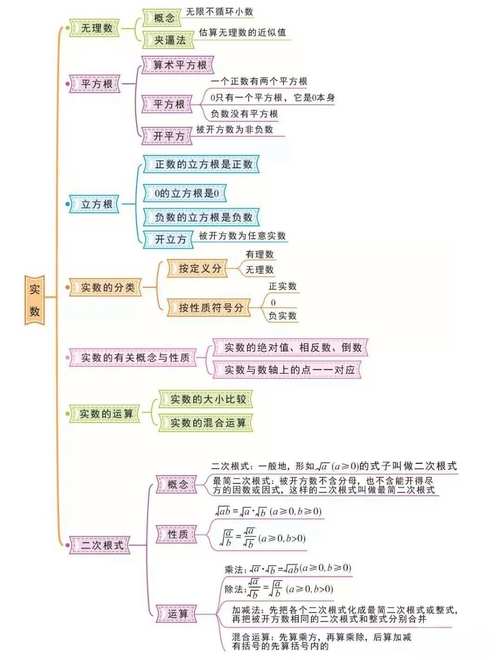
第二章 实数

本章将数的范围从有理数扩展到了实数,是数系的又一次扩充。

核心知识点：

1. 算术平方根:

   
   （图片来源网络，侵删）
   • 定义：如果一个正数 x 的平方等于 a，即 x² = a，x 叫做 a 的算术平方根，记作 √a。
   • 性质： √a ≥ 0（算术平方根具有非负性）；√(a²) = |a|。

2. 平方根:

   • 定义：如果一个数 x 的平方等于 a，即 x² = a，x 叫做 a 的平方根（或二次方根）。
   • 性质： 一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根。

3. 立方根:

   • 定义：如果一个数 x 的立方等于 a，即 x³ = a，x 叫做 a 的立方根，记作 ³√a。
   • 性质： 正数的立方根是正数；负数的立方根是负数；0的立方根是0，任何数都有且只有一个立方根。

4. 实数:

   • 定义： 有理数和无理数统称为实数。
     • 有理数： 可以写成分数形式 m/n（m、n为整数，n≠0）的数，包括整数、有限小数和无限循环小数。
     • 无理数： 无限不循环小数。，√2，√3 等。
   • 实数与数轴： 实数与数轴上的点一一对应，每一个实数都可以用数轴上的一个点来表示，反过来，数轴上的每一个点都表示一个实数。
   • 实数的运算： 有理数的运算法则、运算律（交换律、结合律、分配律）在实数范围内同样适用。

重点与难点：

• 重点： 平方根、立方根的概念和求法；实数的概念和分类。
• 难点：
  • 区分平方根与算术平方根。
  • 理解无理数的概念,识别无理数。
  • 实数运算的准确性,特别是含有根号的运算。

---

第三章 位置的确定

本章引入了平面直角坐标系,是数形结合思想的典型体现，为后续学习函数打下基础。

核心知识点：

1. 平面直角坐标系:

   • 由两条互相垂直、原点重合的数轴构成，水平的数轴称为x轴，铅直的数轴称为y轴。
   • 坐标平面被x轴和y轴分成四个象限。

2. 点的坐标:

   • 坐标平面内的任意一点P,都有唯一的一对有序实数 (x, y) 与之对应，x 叫做点P的横坐标，y 叫做点P的纵坐标。
   • 各象限内点的坐标符号：
     • 第一象限 (, )
     • 第二象限 (, )
     • 第三象限 (, )
     • 第四象限 (, )
   • 坐标轴上的点：
     • x轴上的点,纵坐标为0。
     • y轴上的点,横坐标为0。
     • 原点的坐标是 (0, 0)。

3. 图形与坐标:

   • 用坐标表示地理位置： 选择一个参照点，确定其他点相对于参照点的方向和距离。
   • 用坐标表示平移：
     • 点 (x, y) 向右平移 a 个单位，得到点 (x+a, y)。
     • 点 (x, y) 向左平移 a 个单位，得到点 (x-a, y)。
     • 点 (x, y) 向上平移 b 个单位，得到点 (x, y+b)。
     • 点 (x, y) 向下平移 b 个单位，得到点 (x, y-b)。
     • 图形平移,所有对应点的坐标都按相同规律变化。

重点与难点：

• 重点： 平面直角坐标系的建立；点的坐标的确定；图形平移与坐标变化的关系。
• 难点：
  • 建立适当的坐标系,解决实际问题。
  • 理解并应用平移变换与坐标变化之间的规律。

---

第四章 一次函数

本章是初中函数学习的入门,是本章乃至全书的重中之重。

核心知识点：

1. 函数的概念:

   • 在一个变化过程中,有两个变量 x 和 y，如果对于 x 的每一个确定的值，y 都有唯一确定的值与之对应，那么就说 y 是 x 的函数。x 是自变量，y 是因变量。

2. 正比例函数:

   • 解析式： y = kx (k为常数，k≠0)
   • 图像： 经过原点 (0, 0) 的一条直线。
   • 性质：
     • 当 k > 0 时，图像经过一、三象限，y随x的增大而增大。
     • 当 k < 0 时，图像经过二、四象限，y随x的增大而减小。

3. 一次函数:

   • 解析式： y = kx + b (k, b为常数，k≠0)
   • 图像： 一条直线，当 b=0 时，它就是正比例函数。
   • 性质：
     • k (斜率) 决定直线的倾斜方向和增减性。
       • k > 0，y随x的增大而增大。
       • k < 0，y随x的增大而减小。
     • b (y轴截距) 决定直线与y轴的交点坐标 (0, b)。
   • 两直线平行的条件： k₁ = k₂ 且 b₁ ≠ b₂。

4. 一次函数与方程、不等式的关系:

   • 与一元一次方程： 一次函数 y = kx + b 的图像与x轴的交点的横坐标，就是方程 kx + b = 0 的解。
   • 与一元一次不等式：
     • 不等式 kx + b > 0 的解集，对应函数图像在x轴上方部分的自变量x的取值范围。
     • 不等式 kx + b < 0 的解集，对应函数图像在x轴下方部分的自变量x的取值范围。

5. 待定系数法求一次函数解析式:

   • 步骤： (1) 设；(2) 代；(3) 解；(4) 答，即先设出函数解析式 y = kx + b，然后将已知点的坐标代入，求出 k 和 b 的值。

重点与难点：

• 重点： 一次函数的概念、图像和性质；用待定系数法求解析式；一次函数与方程、不等式的联系。
• 难点：
  • 理解函数的抽象概念。
  • 结合图像理解 k 和 b 的几何意义。
  • 利用一次函数解决复杂的实际问题,如方案选择、最优化问题等。

---

第五章 二元一次方程组

本章是解决含有两个未知数问题的工具,与一次函数联系紧密。

核心知识点：

1. 二元一次方程组:

   • 由两个含有两个未知数的一次方程所组成的方程组。
   • 解： 使方程组中两个方程都成立的未知数的值。

2. 解二元一次方程组的方法:

   • 代入消元法： 将一个方程中的一个未知数用另一个未知数的式子表示出来，代入另一个方程，消去一个未知数。
   • 加减消元法： 通过将两个方程相加或相减，消去一个未知数。
   • 选择原则： 某个未知数的系数为1或-1时，用代入法；同一未知数的系数相同或相反时，用加减法。

3. 三元一次方程组:

   解法思想同样是“消元”，通过代入或加减法，先消去一个未知数，将其转化为二元一次方程组来解。

4. 一次函数与二元一次方程组的关系:

   • 二元一次方程组 ax + by = c 和 dx + ey = f 的解，就是两条直线 y = (-a/b)x + c/b 和 y = (-d/e)x + f/e 的交点的坐标。
   • 无解： 两直线平行（k₁ = k₂，b₁ ≠ b₂）。
   • 有唯一解： 两直线相交。
   • 有无数组解： 两直线重合。

重点与难点：

• 重点： 熟练掌握代入法和加减法解二元一次方程组。
• 难点：
  • 灵活选择消元方法。
  • 解决含有分母、括号或系数为小数的复杂方程组。
  • 理解方程组解的几何意义。

---

第六章 数据的分析

本章学习如何从数据中提取信息,进行科学的分析和判断。

核心知识点：

1. 平均数:

   • 算术平均数： x̄ = (x₁ + x₂ + ... + xₙ) / n
   • 加权平均数： 当数据中各个重要程度不同时，计算出的平均数。x̄ = (x₁·f₁ + x₂·f₂ + ... + xₖ·fₖ) / (f₁ + f₂ + ... + fₖ)，f 代表“权”。

2. 中位数和众数:

   • 中位数： 将一组数据从小到大排列，处在最中间位置的一个数（或最中间两个数的平均数），它不受极端值的影响。
   • 众数： 一组数据中出现次数最多的数据，它不受极端值的影响。

3. 方差:

   • 定义： 各个数据与平均数差的平方的平均数，公式：S² = [ (x₁-x̄)² + (x₂-x̄)² + ... + (xₙ-x̄)² ] / n
   • 意义： 衡量一组数据的波动大小或离散程度。
     • 方差越大,数据的波动越大，越不稳定。
     • 方差越小,数据的波动越小，越稳定。

4. 用样本估计总体:

   • 样本： 从总体中抽取的一部分个体。
   • 总体： 所要考察对象的全体。
   • 抽样调查： 通过样本的特性来估计总体的特性，样本要有代表性。

重点与难点：

• 重点： 平均数、中位数、众数的计算和意义；方差的计算和意义。
• 难点：
  • 理解加权平均数中“权”的含义。
  • 根据具体情境选择合适的统计量（平均数、中位数或众数）来描述数据。
  • 理解方差的意义,并解释其在实际问题中的含义。

---

总结与建议

1. 数形结合： 八年级上册的核心思想是“数形结合”，坐标系将数与形（点、线）联系起来，函数图像直观地展示了数量关系，务必养成画图、看图、用图的习惯。
2. 几何证明入门： 从勾股定理的证明开始，要逐步学习逻辑推理的步骤，做到“言必有据”。
3. 函数思想： 一次函数是函数的起点，要深刻理解“变化”与“对应”的思想，为后续学习反比例函数、二次函数打下坚实基础。
4. 勤加练习： 对于计算（如解方程组、求方差）和证明，必须通过大量练习来达到熟练和准确。

希望这份总结对你有帮助！祝你学习进步！