人教版九年级上册数学圆的核心考点有哪些？

圆的基本概念与性质

圆的定义

• 定义1: 在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所经过的封闭曲线叫做圆，固定的端点O叫做圆心，线段OA叫做半径。
• 定义2: 圆是到定点（圆心）的距离等于定长（半径）的所有点的集合。

与圆有关的概念

• 弦: 连接圆上任意两点的线段。直径是圆中最长的弦，它通过圆心。
• 弧: 圆上任意两点间的部分弧，弧分为优弧（大于半圆）和劣弧（小于半圆）。
• 等圆: 能够重合的两个圆叫做等圆，等圆的半径相等。
• 等弧: 在同圆或等圆中，能够互相重合的弧叫做等弧。

垂径定理及其推论

这是圆中最重要、最核心的定理之一，必须熟练掌握。

• 垂径定理: 垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
  • 图形语言: CD ⊥ AB => AE = EB, AC = CB, AD = DB (其中CD是直径，AB是弦)
• 推论1: 平分弦（非直径）的直径垂直于弦，并且平分弦所对的两条弧。
• 推论2: 弦的垂直平分线经过圆心，并且平分弦所对的两条弧。
• 推论3: 平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

核心思想: 在圆中，直径、弦的垂直平分线、弧的中点连线这“三线”常常是重合的，只要知道其中一条线具有另外两条线的性质，就可以推出其他结论。

圆心角、弧、弦之间的关系

这个定理揭示了圆中三个量之间的等价关系。

• 定理: 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。
• 推论: 在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。
  • 简单记: 圆心角相等 <=> 弧相等 <=> 弦相等 (前提: 同圆或等圆)

圆周角定理

这是另一个核心定理,它将圆周角与圆心角联系起来。

• 定理: 一条弧所对的圆周角等于它所对的圆心角的一半。
  • 图形语言: ∠ACB = 1/2 ∠AOB (其中C是圆上一点，O是圆心)
• 推论1: 同弧或等弧所对的圆周角相等。
• 推论2: 半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。
  • 应用: 这是构造直角三角形的重要方法，"直径所对的圆周角是直角"。
• 推论3: 如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

---

第二部分：点、直线、圆与圆的位置关系

点与圆的位置关系

设圆的半径为 r，点到圆心的距离为 d。

• 点在圆外 ⇔ d > r
• 点在圆上 ⇔ d = r
• 点在圆内 ⇔ d < r

重要结论: 不在同一直线上的三个点确定一个圆。

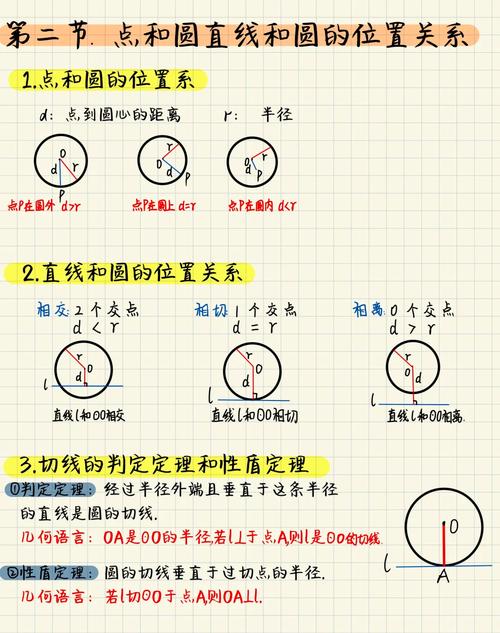
直线与圆的位置关系

设圆的半径为 r，圆心到直线的距离为 d。

• 相离: 直线与圆没有公共点 ⇔ d > r
• 相切: 直线与圆有唯一公共点（切点）⇔ d = r
• 相交: 直线与圆有两个公共点 ⇔ d < r

切线的性质与判定:

• 性质定理: 圆的切线垂直于经过切点的半径。
  • 应用: 证明垂直关系，计算切线长度。
• 判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线。
  • 应用: 证明一条直线是圆的切线，关键步骤是“连半径，证垂直”。
• 切线长定理: 从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。
  • 图形语言: PA, PB 是切点 => PA = PB, ∠APO = ∠BPO

圆与圆的位置关系

设两圆的半径分别为 R 和 r (R ≥ r)，圆心距为 d。

• 外离: d > R + r (无公共点)
• 外切: d = R + r (唯一公共点，外切点)
• 相交: R - r < d < R + r (两个公共点)
• 内切: d = R - r (唯一公共点，内切点)
• 内含: d < R - r (无公共点)
• 同心圆: d = 0 (内含的特殊情况)

相交两圆的性质: 相交两圆的连心线垂直平分两圆的公共弦。

---

第三部分：正多边形与圆

正多边形与圆的关系

• 定义: 各边相等，各角也相等的多边形叫做正多边形。
• 关系: 任何一个正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆，这个共同的圆心叫做正多边形的中心。

正多边形的计算

正多边形的计算通常转化为解由它的中心、顶点和边心距构成的直角三角形来解决。

• 中心角: 正多边形每一边所对的圆心角。α = 360° / n (n为边数)
• 半径: 正多边形外接圆的半径。
• 边心距: 正多边形内切圆的半径，即中心到边的距离。
• 边长: 正多边形的边长。

核心公式: 在由中心、顶点和边心距构成的直角三角形中：

• 边心距 r = R * cos(α/2) = R * cos(180°/n)
• 边长 a = 2 * R * sin(α/2) = 2 * R * sin(180°/n)
• 周长 P = n * a
• 面积 S = 1/2 周长 边心距 = 1/2 P r

---

第四部分：弧长和扇形的面积

弧长公式

在半径为 R 的圆中，因为圆的周长 C = 2πR，所以圆心角为 n° 的弧长 l 的计算公式为： l = (n/360) * 2πR = (nπR)/180

扇形面积公式

在半径为 R 的圆中，圆心角为 n° 的扇形面积 S 的计算公式为： S = (n/360) * πR²

弓形面积

弓形是由弦和它所对的弧组成的图形。

• 优弓形面积 = 扇形面积 + 三角形面积
• 劣弓形面积 = 扇形面积 - 三角形面积

圆锥的侧面积和全面积:

• 圆锥的侧面展开图是一个扇形。
• 圆锥的母线 l 就是展开后扇形的半径。
• 圆锥的底面半径 r 就是展开后扇形的弧长所对应的圆的半径。
• 圆锥的底面周长 C = 2πr，它等于侧面展开图扇形的弧长 l。
• 圆锥的侧面积 S_侧 = (1/2) * 扇形弧长 * 扇形半径 = (1/2) * 2πr * l = πrl
• 圆锥的全面积 S_全 = S_侧 + S_底 = πrl + πr²

---

学习建议

1. 数形结合: 圆是几何图形，一定要结合图形来理解和记忆定理，自己动手画图，观察图形中的关系。
2. 掌握核心定理: 垂径定理、圆周角定理、切线的判定与性质是本章的基石，必须做到烂熟于心，并能灵活运用。
3. 规范解题: 在证明题中，要写出“∵... ∴...”的推理过程，特别是切线的证明，步骤要清晰（连半径→证垂直）。
4. 分类讨论思想: 在处理位置关系（点、线、圆与圆）时，要注意分情况讨论，不要遗漏。
5. 多加练习: 通过做一些典型的例题和习题，巩固所学知识，特别是综合性较强的题目，如动点问题、与函数结合的问题等。

希望这份详细的梳理能帮助你更好地学习《圆》这一章！加油！