九年级数学旋转教案如何突破教学难点？

九年级数学《旋转》教案：从入门到精通，让抽象概念“动”起来！

资深教师独家整理，含教学目标、重难点、互动设计与经典例题，备课无忧，教学高效！）**

---

引言：为什么《旋转》是九年级数学的“分水岭”？

各位同仁、亲爱的同学们,大家好！

在九年级数学的几何世界里，《旋转》无疑是一座重要的里程碑，它不仅是对之前所学的全等变换（平移、轴对称）的深化与拓展，更是连接平面几何与后续解析几何、函数思想的桥梁，许多同学初次接触旋转时，常常感到抽象难懂，对“旋转中心”、“旋转角”、“对应点”等概念模糊不清。

作为深耕一线教育多年的专家，我深知教学的痛点与难点，今天我将为大家呈上一份精心打磨的九年级数学《旋转》教案，旨在通过生动有趣的教学设计，将抽象的“旋转”概念变得直观可感，帮助学生们轻松突破难关，真正实现从“听懂”到“会用”再到“精通”的跨越。

---

本课教学设计详案

【课题】 23.1 旋转（第一课时）

【授课年级】 九年级

【教材分析】 本节课是人教版九年级数学上册第二十三章的核心内容，学生在学习了平移和轴对称的基础上，进一步学习图形的旋转，旋转是图形变换的基本形式之一，它刻画了图形运动的核心特征，本节课的重点是理解旋转的定义和性质，为后续学习中心对称、图形的综合应用以及解析几何中的坐标变换奠定坚实基础。

【学情分析】 九年级学生已经具备了一定的几何直观和逻辑推理能力，对图形的运动有初步的认识，但旋转比平移和轴对称更复杂，涉及到角度和方向，学生可能会在确定旋转要素、理解旋转性质时遇到困难，教学中应充分利用多媒体动画和动手操作,帮助学生建立直观表象。

【教学目标】

1. 知识与技能：
   • 理解旋转的定义，掌握旋转的三个基本要素：旋转中心、旋转方向、旋转角。
   • 掌握旋转的基本性质：旋转前后的图形全等；对应点到旋转中心的距离相等；任意一对对应点与旋转中心所连线段的夹角等于旋转角。
2. 过程与方法：
   • 通过观察、操作、归纳等数学活动，经历探索旋转性质的过程,培养学生的几何直观和抽象思维能力。
   • 学习运用旋转的性质解决简单的几何问题,体会数形结合的思想。
3. 情感态度与价值观：
   • 在探索活动中感受图形变换的奇妙与和谐,激发学习数学的兴趣。
   • 通过小组合作与交流,培养合作精神和严谨的治学态度。

【教学重难点】

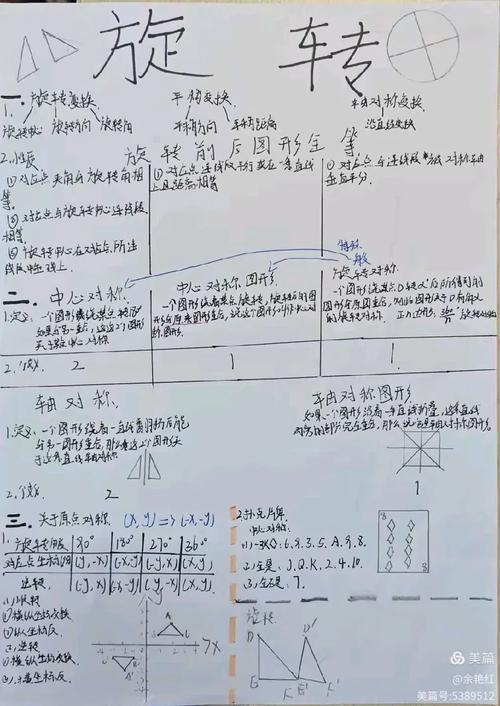
• 教学重点： 旋转的定义和性质。
• 教学难点： 理解并准确运用旋转的性质，特别是“对应点与旋转中心所连线段的夹角等于旋转角”这一性质。

【教学方法】 情境教学法、启发式教学法、小组合作探究法、多媒体辅助教学法。

【教学准备】 教师：PPT课件、几何画板动画、三角板、量角器。 学生：预习课本、练习本、铅笔、直尺、量角器、一张硬纸片和图钉。

---

教学过程：环环相扣，层层深入

第一环节：情境导入，激发兴趣 (约5分钟)

• 教师活动：

  1. 播放一段视频或展示一组图片：钟表的指针、风车的转动、汽车方向盘的旋转、游乐园里的摩天轮等。
  2. 提问：“同学们，这些物体的运动有什么共同的特点？”（引导学生说出“绕着一个点或轴转动”）
  3. 追问：“它们是简单的平移吗？是沿某条直线对折形成的轴对称吗？”（否定，引出新的概念——旋转）
  4. 板书课题： 23.1 旋转

• 设计意图： 从生活实例入手，创设生动有趣的教学情境，让学生直观感受旋转现象，激发探究新知的欲望,自然地引入课题。

第二环节：动手操作，探究新知 (约15分钟)

• 制作“旋转小风车”

  1. 学生活动： 每位学生拿出硬纸片和图钉，将一个三角形（或任意图形）用图钉固定在纸片上，作为“风车叶片”。
  2. 教师引导： “请同学们用手拨动你的‘风车’，观察它是如何运动的，想一想，要让这个图形旋转起来，必须确定哪些要素？”
  3. 小组讨论与归纳：
     • 旋转中心： 图钉固定的那个点（板书）。
     • 旋转方向： 顺时针或逆时针（板书）。
     • 旋转角： 图形转动的角度（板书）。
  4. 教师总结： 像这样，把一个图形绕着某一点O转动一个角度，这种图形变换叫做旋转，点O叫做旋转中心，转动的角叫做旋转角，如果旋转方向是顺时针，旋转角为正；逆时针，旋转角为负。（为高中学习做铺垫）

• 探索旋转的性质

  1. 教师演示： 使用几何画板，演示一个三角形△ABC绕点O旋转一定角度得到△A'B'C'。
  2. 学生探究： 观察动画，小组合作完成以下任务：
     • 任务1：测量△ABC和△A'B'C'的形状、大小，你发现了什么？（全等）
     • 任务2：连接AO、A'O，BO、B'O，CO、C'O，分别测量它们的长度，你发现了什么？（对应点到旋转中心的距离相等）
     • 任务3：测量∠AOA'、∠BOB'、∠COC'的大小，你发现了什么？（它们都等于旋转角）
     • 任务4：测量∠AOB和∠A'OB'的大小，你发现了什么？（相等）
  3. 师生共同总结旋转的性质（板书）：
     • 性质1：旋转前后的图形是全等图形。
     • 性质2：任意一对对应点与旋转中心所连线段的夹角都等于旋转角。
     • 性质3：对应点到旋转中心的距离相等。

• 设计意图： 通过“做中学”，让学生亲身经历知识的发生、发展过程，从具体操作到抽象概括，符合学生的认知规律，有效突破教学难点,使学生对旋转的性质理解得更加深刻透彻。

第三环节：例题精讲，学以致用 (约15分钟)

• 例1（基础应用）： 如图，△ABC是等边三角形，D是BC边上一点，△ABD经过旋转后得到△ACE。 (1) 旋转中心是哪一点？ (2) 旋转了多少度？ (3) 如果M是AD的中点，那么经过上述旋转后，点M的对应点M'在哪里？

  • 师生共析：
    • (1) 旋转中心是点A。
    • (2) 因为△ABC是等边三角形，∠BAC=60°，根据旋转性质，∠BAC就是旋转角，所以旋转了60°。
    • (3) 点M的对应点是线段AE的中点M'。

• 例2（能力提升）： 如图，在正方形ABCD中，E是CD边上一点，将△ADE绕点A顺时针旋转90°到△ABF的位置。 (1) 指出旋转中心。 (2) 求∠DAF的度数。 (3) 如果正方形的边长为4，DE=1,求EF的长度。

  • 师生共析：
    • (1) 旋转中心是点A。
    • (2) 旋转角为90°，即∠EAF=90°，因为∠DAB=90°，DAF = ∠DAB - ∠BAF = 90° - ∠DAE = ∠EAF = 90°。（此问有多种思路,引导学生一题多解）
    • (3) 由旋转性质可知，△ADE ≌ △ABF，所以AF=AE, ∠DAE=∠BAF，在Rt△ADE中，AE=√(AD²+DE²)=√(4²+1²)=√17，在Rt△AEF中，∠EAF=90°，EF=√(AE²+AF²)=√(17+17)=√34。

• 设计意图： 例题设计由浅入深，层层递进，例1巩固基础概念，例2则综合考查旋转性质与勾股定理等知识，旨在培养学生综合运用知识解决问题的能力,并渗透数形结合的思想。

第四环节：课堂小结，巩固提升 (约5分钟)

• 学生活动： 请学生谈谈本节课的收获和体会。

• 教师总结：

  1. 我们今天学习了什么？（旋转的定义、三要素、三个性质）
  2. 解决旋转问题的关键是什么？（找准旋转中心、旋转角和对应点,灵活运用性质）
  3. 数学思想：我们再次体会了“从具体到抽象”、“数形结合”的数学思想。

• 布置作业：

  1. 基础题： 课本P79 练习第1、2题。
  2. 提高题： 课本P80 习题23.1 第3、4题。
  3. 拓展题： 利用旋转设计一个美丽的图案,并说明你的设计思路。

• 设计意图： 回顾本节课的核心内容，形成知识网络，分层作业满足不同层次学生的需求，既巩固了基础,又为学生提供了探索和创造的空间。

---

教学反思与拓展

本节课的设计力求体现学生的主体地位，通过“情境-探究-应用-的模式，引导学生主动建构知识，多媒体的运用使抽象的旋转过程变得直观,动手操作则加深了学生的理解。

拓展思考：

1. 旋转与坐标： 在平面直角坐标系中，如果一个图形绕原点旋转90°或180°，其顶点坐标会遵循怎样的规律？（为后续学习埋下伏笔）
2. 旋转的应用： 旋转在工程设计、艺术创作、计算机图形学（如游戏动画）中有着广泛的应用，可以鼓励学生课后搜集相关资料,感受数学的实用价值。

---

写在最后：给教师和同学们的建议

• 给教师： 教学是一门艺术，教案是蓝图，在实际教学中，请根据您班级学生的具体情况进行灵活调整，多一些鼓励，少一些批评，让学生在探索中犯错，在纠错中成长,这才是数学教育的真谛。
• 给同学： 学习《旋转》不可怕，关键在于“动”起来！亲手画一画、剪一剪、转一转，你会发现旋转的规律其实很简单，每一个复杂的图形变换，都是由最简单的性质构成的，掌握了它们,你就能轻松驾驭！

希望这份详尽的九年级数学《旋转》教案能对您的教学或学习有所帮助，如果您有任何问题或不同的见解，欢迎在评论区留言交流，让我们一起探讨,共同进步！

---

#九年级数学 #旋转教案 #初中数学 #教学设计 #数学思维 #几何变换 #教师必备 #学习技巧