八年级上册第一次月考数学考什么？

下面我为你梳理一下这次月考的核心考点、常见题型、备考建议和模拟题，希望能帮助你高效复习，取得好成绩！

---

核心考点分析

八年级上册第一次月考主要围绕两大核心章节：三角形和全等三角形。

第一章《三角形》考点

1. 三角形的边与角

   • 三边关系定理：任意两边之和大于第三边，任意两边之差小于第三边，这是判断三条线段能否构成三角形的依据。
   • 三角形的内角和定理：三个内角的和等于180°。
   • 三角形的外角性质：三角形的一个外角等于与它不相邻的两个内角的和；三角形的一个外角大于任何一个与它不相邻的内角。
   • 三角形的分类：按角分为锐角、直角、钝角三角形；按边分为不等边、等腰（含等边）三角形。

2. 多边形

   • 内角和公式：n边形的内角和为 (n-2) × 180°。
   • 外角和定理：任意多边形的外角和都等于360°。
   • 正多边形：各边相等，各角也相等的多边形。

第二章《全等三角形》考点 (本章节是重中之重)

1. 全等三角形的概念与性质

   • 定义：能够完全重合的两个三角形叫做全等三角形。
   • 性质：全等三角形的对应边相等，对应角相等。

2. 全等三角形的判定方法 (核心中的核心)

   
   （图片来源网络，侵删）
   • SSS (边边边)：三边对应相等的两个三角形全等。
   • SAS (边角边)：两边和它们的夹角对应相等的两个三角形全等。
   • ASA (角边角)：两角和它们的夹边对应相等的两个三角形全等。
   • AAS (角角边)：两角和其中一个角的对边对应相等的两个三角形全等。
   • HL (斜边、直角边)：斜边和一条直角边对应相等的两个直角三角形全等。（这是Rt△特有的判定方法）
   • 易错点：“SSA” 和 “AAA” 不能判定两个三角形全等！

3. 角平分线的性质

   • 性质定理：角平分线上的点到角两边的距离相等。
   • 判定定理：到一个角两边的距离相等的点，在这个角的平分线上。

4. 全等三角形的应用

   • 证明线段相等：证明它们是全等三角形的对应边。
   • 证明角相等：证明它们是全等三角形的对应角。
   • 证明线段平行或垂直：通过证明角相等（如内错角、同位角相等）来实现。

---

常见题型与解题技巧

1. 选择题/填空题

   • 题型：考察基础概念、定理的直接应用。
   • 例子：
     • 给出四条线段长度,判断能组成三角形的有几个。
     • 已知三角形两个角,求第三个角或未知角的度数。
     • 根据已知条件,判断两个三角形是否全等（直接套用判定方法）。
   • 技巧：概念清晰，公式记牢，细心计算。

2. 计算题

   
   （图片来源网络，侵删）
   • 题型：利用三角形或多边形的内角和、外角和公式进行计算。
   • 例子：
     • 已知一个多边形的内角和为1080°，求它的边数。
     • 在一个三角形中,已知∠A=2∠B，∠C=90°，求∠A、∠B的度数。
   • 技巧：设未知数，列方程是解决这类问题的常用方法。

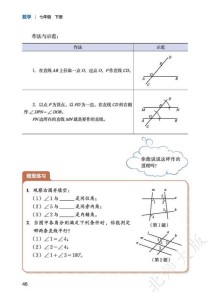
3. 作图题

   • 题型：基本作图，如作一个角等于已知角、作已知线段的垂直平分线、作已知角的角平分线。
   • 技巧：步骤清晰，痕迹保留，最后要有结论性的语言（如“射线OC就是∠AOB的角平分线”）。

4. 证明题 (压轴题，也是难点)

   • 题型：全等三角形综合证明，常结合角平分线、垂直、中点等条件。
   • 解题步骤（黄金法则）：
     1. 读题：仔细审题，明确已知条件和求证结论。
     2. 画图：根据题意画出准确的几何图形，并在图上标出已知条件。
     3. 分析：这是最关键的一步！从求证结论出发，倒着想：要证明两条线段相等（或两个角相等），需要证明哪两个三角形全等？再看这两个三角形已经具备了哪些条件（边、角），还缺什么条件？想办法利用已知条件补上这个“缺口”。
     4. 书写：按照“∵... ∴...”的格式规范书写证明过程，每一步都要有理有据（如：∵ 在△ABC和△DEF中， AB=DE (已知)， ∠B=∠E (已知)， BC=EF (已知) ∴ △ABC ≌ △DEF (SAS)）。
   • 技巧：
     • “截长补短”法：遇到证明线段和差关系（如 AB = CD + EF）时，常用此法。
     • 倍长中线法：题目中出现中点时，延长中线，构造全等三角形是经典思路。
     • 公共边、公共角：在图中要善于发现隐藏的公共边或公共角，它们常常是全等的条件。

---

备考建议

1. 回归课本，夯实基础：把课本上的概念、定理、公理重新看一遍，确保理解无误，特别是全等三角形的五个判定方法，要做到脱口而出。
2. 整理错题，查漏补缺：把平时作业和练习中的错题整理到错题本上，分析错误原因（是概念不清？还是粗心大意？），定期回顾。
3. 专题训练，攻克难点：针对“证明题”这个难点，找一些典型的例题和习题进行专项练习，熟练掌握分析思路和书写格式。
4. 规范作答，细节取胜：考试时，尤其是证明题，书写一定要规范，每一步推理都要有依据，图形要清晰，标号要准确，步骤分很重要，即使最后结论没证出来，清晰的步骤也能拿到大部分分数。
5. 调整心态，沉着应考：遇到难题不要慌，先跳过，把会做的题的分数拿到手再回头攻克难题。

---

模拟题自测

（一）选择题 (每题3分，共24分)

1. 下列长度的三条线段,能组成三角形的是 ( ) A. 1, 2, 3 B. 2, 3, 4 C. 3, 4, 8 D. 4, 5, 10

2. 在△ABC中，∠A=55°，∠B=65°，则∠C的度数为 ( ) A. 50° B. 60° C. 70° D. 80°

3. 下列条件中,不能判定△ABC ≌ △DEF的是 ( ) A. AB=DE, ∠A=∠D, AC=DF B. AB=DE, ∠B=∠E, BC=EF C. ∠A=∠D, ∠B=∠E, AB=DE D. AB=DE, ∠B=∠E, BC=DF

4. 如图,点C是AB的中点，CD⊥AB，DE⊥AC，DF⊥BC，则下列结论不一定成立的是 ( ) (此处应有图，描述为：C是AB中点，CD垂直于AB，D在AB上，E在AC上，DE垂直于AC，F在BC上，DF垂直于BC) A. DE = DF B. ∠ADC = 90° C. AE = BF D. CD是∠ACB的角平分线

（二）填空题 (每题3分，共21分)

5. 一个多边形的内角和是它外角和的2倍,则这个多边形是____边形。

6. 如图,AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，若S△ABD = 10，AB = 5，则DE = __。 (此处应有图，描述为：AD是角平分线，E在AB上，DE垂直AB，F在AC上，DF垂直AC)

7. 如图,点B、E、C、F在同一直线上，AB=DE，∠B=∠E，BC=EF，请添加一个条件，使△ABC ≌ △DEF，这个条件可以是__。 (此处应有图，描述为：B, E, C, F共线，A在B上方，D在E上方，连接AD)

（三）解答题 (共55分)

8. (8分) 在△ABC中，已知∠A=40°，∠B=∠C，求∠C的度数。

9. (10分) 如图，AC=AD，∠BAC=∠BAD，求证：BC=BD。 (此处应有图，描述为：点A在上方，B、C、D在下方，C和D在B的两侧，连接AC, AD, BC, BD)

10. (12分) 如图，AC⊥BC，AD⊥BD，垂足分别为C、D，AD=BC，求证：∠DAB=∠CBA。 (此处应有图，描述为：A和B是两个点，C是A下方垂足，D是B下方垂足，连接AD, BC)

11. (15分) 如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F，且DE=DF。 (1) 求证：AD是∠BAC的角平分线。 (2) 若AB=6，AC=10，求线段EF的长度。 (此处应有图，描述为：D是BC中点，E在AB上，DE垂直AB，F在AC上，DF垂直AC)

---

参考答案

选择题

1. B (2+3>4, 2+4>3, 3+4>2)
2. B (180° - 55° - 65° = 60°)
3. D (SSA不能判定)
4. C (不一定成立，除非AC=BC)

填空题 5. 六 (设边数为n，则 (n-2)×180° = 2×360°，解得n=6) 6. 4 (S△ABD = 1/2 AB DE = 10，DE = 10 * 2 / 5 = 4) 7. AC=DF 或 ∠ACB=∠DEF (答案不唯一，只要能补充成SAS、ASA或AAS即可)

解答题

8. 解： ∵ 在△ABC中，∠A + ∠B + ∠C = 180° (三角形内角和定理) 又∵ ∠B = ∠C (已知)，∠A = 40° (已知) ∴ 40° + ∠C + ∠C = 180° ∴ 2∠C = 140° ∴ ∠C = 70°

9. 证明： 在△ABC和△ABD中， ∵ { AC = AD (已知) { ∠BAC = ∠BAD (已知) { AB = AB (公共边) ∴ △ABC ≌ △ABD (SAS) ∴ BC = BD (全等三角形的对应边相等)

10. 证明： ∵ AC⊥BC，AD⊥BD (已知) ∴ ∠ACB = ∠ADB = 90° 在△ACB和△ADB中， ∵ { ∠ACB = ∠ADB (已证) { AD = BC (已知) { AB = AB (公共边) ∴ △ACB ≌ △ADB (HL) ∴ ∠DAB = ∠CBA (全等三角形的对应角相等)

11. 证明： (1) ∵ DE⊥AB，DF⊥AC (已知) ∴ ∠AED = ∠AFD = 90° 在Rt△AED和Rt△AFD中， ∵ { AD = AD (公共边) { DE = DF (已知) ∴ Rt△AED ≌ Rt△AFD (HL) ∴ ∠EAD = ∠FAD (全等三角形的对应角相等) 即 AD是∠BAC的角平分线。

    (2) ∵ AD是∠BAC的角平分线 (已证) 且 DE⊥AB，DF⊥AC (已知) ∴ DE = DF (角平分线上的点到角两边的距离相等) ∵ D是BC的中点 (已知) ∴ BD = DC 在△BDE和△CDF中， ∵ { ∠DEB = ∠DFC = 90° (已知) { DE = DF (已证) { ∠BDE = ∠CDF (对顶角相等) ∴ △BDE ≌ △CDF (AAS) ∴ BE = CF (全等三角形的对应边相等) ∵ AB = 6，AC = 10 ∴ AE = AB - BE = 6 - BE AF = AC - CF = 10 - CF ∵ BE = CF ∴ AF - AE = (10 - CF) - (6 - BE) = 10 - 6 - CF + BE = 4 又 ∵ AE = AF (由(1)可知Rt△AED ≌ Rt△AFD) 设 AE = AF = x 则 x - x = 4 (此路不通，换思路) 正确思路： ∵ AE = AF (由(1)可知) ∴ EF = AF - AE 又 ∵ BE = CF (已证) ∴ EF = (AC - CF) - (AB - BE) = AC - AB - CF + BE = 10 - 6 + (BE - CF) = 4 + 0 = 4 ∴ 线段EF的长度为4。

希望这份详细的总结和模拟题能对你有所帮助！祝你月考顺利，取得优异的成绩！加油！