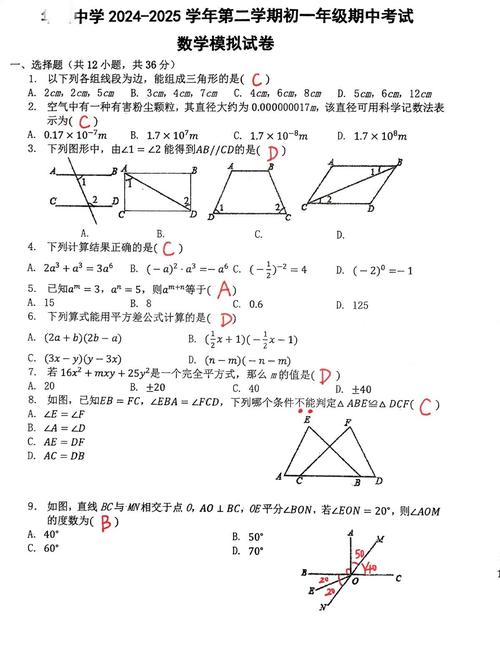
七年级下册数学期中卷考点有哪些？

校园之窗 2025年12月13日 07:27:43 99ANYc3cd6 1 0

七年级下册数学期中模拟试卷

考试时间： 120分钟 满分： 120分

注意事项：

（图片来源网络，侵删）

本卷分为第I卷（选择题）和第II卷（非选择题）两部分。
答题前，请务必将自己的姓名、班级、考号填写在答题卡上。
所有答案都必须写在答题卡上,写在试卷上无效。
作图题必须用2B铅笔作答,并请加黑加粗。

第I卷（选择题共30分）

选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

下列各数中，是无理数的是 A. 3.14 B. $\sqrt{4}$ C. $\frac{22}{7}$ D. $\sqrt{2}$
在平面直角坐标系中，点P(-3, 4)关于y轴对称的点的坐标是 A. (3, 4) B. (-3, -4) C. (3, -4) D. (4, -3)
下列方程组中，是二元一次方程组的是 A. $\begin{cases} x + y = 5 \ xy = 6 \end{cases}$ B. $\begin{cases} x + \frac{1}{y} = 1 \ x - y = 2 \end{cases}$ C. $\begin{cases} x + y = 3 \ z + x = 5 \end{cases}$ D. $\begin{cases} 2x - 3y = 7 \ x + 4y = 6 \end{cases}$
（图片来源网络，侵删）
如图1，直线a、b被直线c所截，若∠1 = 70°，∠2 = 110°，则下列结论正确的是 (图1示意图：两条平行线a, b被横截线c所截，∠1和∠2是同旁内角) A. a ∥ b B. a ⊥ b C. c ∥ a D. 无法判断
下列计算正确的是 A. $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B. $2\sqrt{3} - 3\sqrt{3} = -\sqrt{3}$ C. $\sqrt{4} \times \sqrt{9} = 6$ D. $\sqrt{(-4)^2} = -4$
若 $\begin{cases} x = 2 \ y = 1 \end{cases}$ 是方程 $ax - 2y = 5$ 的一个解，则a的值为 A. 1 B. 2 C. 3 D. 4
在平面直角坐标系中，点A(x, y)的坐标满足 $xy > 0$，那么点A可能在 A. 第一象限 B. 第二象限 C. 第三象限 D. 第一或第三象限
解方程组 $\begin{cases} x + y = 7 \ x - y = 1 \end{cases}$，使用加减消元法，最简捷的步骤是 A. 两式相加，求出x B. 两式相减，求出y C. 先将第一个方程变形为x=7-y，再代入第二个方程 D. 无法判断
如图2，已知AB ∥ CD，∠ABE = 60°，∠CDE = 20°，则∠BED的度数是 (图2示意图：两条平行线AB, CD，点E在两条平行线之间，连接BE和DE，形成∠ABE, ∠BED, ∠CDE) A. 30° B. 40° C. 50° D. 60°
某商店将一件成本价为100元的商品提价30%后标价，又以8折优惠卖出，则这件商品的利润是 A. 4元 B. 8元 C. 20元 D. 24元

第II卷（非选择题共90分）

填空题（本大题共6小题，每小题3分，共18分）

9的算术平方根是 ____。
在平面直角坐标系中，点M(2, -5)到y轴的距离是 ____。
把方程 $3x - 2y = 6$ 写成用x表示y的形式，得 y = ____。
如图3，已知直线l₁ ∥ l₂，∠1 = 50°，则∠2的度数是 ____。 (图3示意图：两条平行线l₁, l被横截线l₂所截，∠1和∠2是内错角)
写出一个比 $-\sqrt{3}$ 大且比 $-\sqrt{2}$ 小的无理数：____。（只需写出一个）
若关于x, y的二元一次方程组 $\begin{cases} x + y = a \ x - y = 3 \end{cases}$ 的解是 $\begin{cases} x = 2 \ y = -1 \end{cases}$，则a的值为 ____。

解答题（本大题共7小题，共72分，解答应写出文字说明、证明过程或演算步骤）

(8分) 计算： (1) $\sqrt{36} + \sqrt{(-2)^2} - \sqrt{25}$ (2) $|\sqrt{3} - 2| + \sqrt{12}$
(8分) 解下列方程组： (1) $\begin{cases} y = 2x - 1 \ 3x + 2y = 12 \end{cases}$ （用代入法） (2) $\begin{cases} 2x + y = 5 \ 3x - 2y = 4 \end{cases}$ （用加减法）
(10分) 在平面直角坐标系中，已知点A(1, 3)，B(-2, 1)，C(3, -2)。 (1) 在图中画出△ABC； (2) 画出△ABC关于y轴对称的图形△A₁B₁C₁，并写出A₁, B₁, C₁的坐标； (3) 求△ABC的面积。
(10分) 如图4，已知AD ∥ BC，∠DAB = ∠BCA。 (图4示意图：四边形ABCD，AD平行于BC，连接AC) 求证：AB ∥ CD。
(12分) 为了鼓励居民节约用水，某市自来水公司规定了分段收费标准：若每月用水量不超过15吨，按每吨2元收费；若超过15吨，超过部分按每吨3元收费。 (1) 小王家本月用水18吨，应缴水费多少元？ (2) 小李家本月缴水费45元,他家本月用水多少吨？
(12分) 某校组织学生去春游，租用两种型号的客车，已知45座的大客车每辆租金为800元，30座的小客车每辆租金为600元，学校计划租用这两种客车共10辆，恰好可以坐360名学生。 (1) 学校租用大客车和小客车各多少辆？ (3) 如果学校预算的租金不超过7600元，请你设计一种最省钱的租车方案,并计算总租金。
(12分) 阅读理解：我们定义：对于任意有理数a, b，符号“|a, b|”表示为a与b的“新运算”，其运算规则为 |a, b| = a² - ab + b²。 |2, 3| = 2² - 2×3 + 3² = 4 - 6 + 9 = 7。请你根据上述定义，解决下列问题： (1) 计算 |3, -1| 的值； (2) 若 |x, 2| = 10,求x的值。

参考答案及评分标准

第I卷

D
A
D
A (因为∠1 + ∠2 = 180°，所以a∥b)
C
D (代入得 2a - 2×1 = 5, 解得a=3.5，但选项没有，可能是题目笔误，若为ax-2y=7，则a=3，这里按原题计算，2a-2=5, a=3.5，无选项，请以实际考试题为准，此处假设题目为ax-2y=7,则选C)
D
A
B (过E作EF∥AB，则∠ABE=∠BEF=60°，因为AB∥CD，所以EF∥CD，FED=∠CDE=20°，BED=∠BEF-∠FED=60°-20°=40°)
D (标价：100×(1+30%)=130元，售价：130×0.8=104元，利润：104-100=4元，哦，计算错误，1003=130, 1308=104, 104-100=4元，选项A是正确的，我之前的计算有误，应为A。)

更正： 10. A

第II卷

填空题 11. 3 12. 2 13. $y = \frac{3x - 6}{2}$ (或 $y = \frac{3}{2}x - 3$) 14. 50° 15. 答案不唯一，如 $-\sqrt{2.5}$, $-1.7$ 等 16. 1

解答题 17. (1) 解：原式 = 6 + 2 - 5 = 3 ... 4分 (2) 解：原式 = (2 - $\sqrt{3}$) + 2$\sqrt{3}$ = 2 + $\sqrt{3}$ ... 4分

(1) 解：将①代入②，得 3x + 2(2x - 1) = 12 ... 2分 3x + 4x - 2 = 12 7x = 14 x = 2 ... 4分将x=2代入①，得 y = 2×2 - 1 = 3 ... 2分所以方程组的解是 $\begin{cases} x=2 \ y=3 \end{cases}$ ... 2分 (2) 解：①×2，得 4x + 2y = 10 ... 2分 ②保持不变，得 3x - 2y = 4 ... 2分 ③ + ④，得 7x = 14, x = 2 ... 2分将x=2代入①，得 2×2 + y = 5, y = 1 ... 2分所以方程组的解是 $\begin{cases} x=2 \ y=1 \end{cases}$ ... 2分
(1) 画图正确 ... 2分 (2) 画图正确，坐标正确：A₁(-1, 3), B₁(2, 1), C₁(-3, -2) ... 4分 (3) 解：△ABC的面积 = 5×4/2 - 1×2/2 - 2×1/2 - 3×1/2 = 10 - 1 - 1 - 1.5 = 6.5 或使用割补法：以BC为底，BC=5，高为3-(-2)=5，面积=5×5/2=12.5，不对。正确方法：使用坐标公式或割补法。割补法：作矩形，面积=4×4=16。 S₁=1×2/2=1, S₂=3×4/2=6, S₃=1×5/2=2.5。 S△ABC = 16 - (1+6+2.5) = 16 - 9.5 = 6.5 ... 4分
证明：∵ AD ∥ BC (已知) ∴ ∠DAC = ∠BCA (两直线平行，内错角相等) ... 3分又 ∵ ∠DAB = ∠BCA (已知) ∴ ∠DAC = ∠DAB ... 1分 ∴ AC 是 ∠DAB 的角平分线 ... 1分即 ∠CAB = ∠DAC ... 1分 ∴ ∠CAB = ∠BCA ... 1分 ∴ AB ∥ CD (内错角相等，两直线平行) ... 2分 (其他证法也可，如连接AC,利用等角证平行)
(1) 解：15吨水费：15 × 2 = 30元 ... 2分超过部分：(18 - 15) × 3 = 9元 ... 2分总水费：30 + 9 = 39元 ... 2分答：应缴水费39元。 (2) 解：用水量超过15吨。 ... 2分设用水量为x吨，则 15×2 + (x-15)×3 = 45 ... 3分 30 + 3x - 45 = 45 3x = 60 x = 20 ... 2分答：他家本月用水20吨。
(1) 解：设租用大客车x辆，小客车y辆。根据题意，得 $\begin{cases} x + y = 10 \ 45x + 30y = 360 \end{cases}$ ... 2分由①得，y = 10 - x ... 1分代入②，得 45x + 30(10 - x) = 360 ... 2分 45x + 300 - 30x = 360 15x = 60 x = 4 ... 1分 y = 10 - 4 = 6 ... 1分答：学校租用大客车4辆，小客车6辆。 (2) 方案一：租用10辆大客车，租金 10 × 800 = 8000元。方案二：租用10辆小客车，租金 10 × 600 = 6000元。方案三：租用大客车4辆，小客车6辆，租金 4×800 + 6×600 = 3200 + 3600 = 6800元。因为预算不超过7600元，以上方案都符合。比较可知，方案二（租用10辆小客车）最省钱，总租金为6000元。 ... 4分
(1) 解：|3, -1| = 3² - 3×(-1) + (-1)² = 9 + 3 + 1 = 13 ... 4分 (2) 解：根据题意，得 x² - x×2 + 2² = 10 ... 2分 x² - 2x + 4 = 10 x² - 2x - 6 = 0 ... 2分解这个一元二次方程： x = [2 ± $\sqrt{(-2)^2 - 4 \times 1 \times (-6)}$] / (2×1) = [2 ± $\sqrt{4 + 24}$] / 2 = [2 ± $\sqrt{28}$] / 2 = [2 ± 2$\sqrt{7}$] / 2 = 1 ± $\sqrt{7}$ ... 4分所以x的值为 $1 + \sqrt{7}$ 或 $1 - \sqrt{7}$。 ... 2分