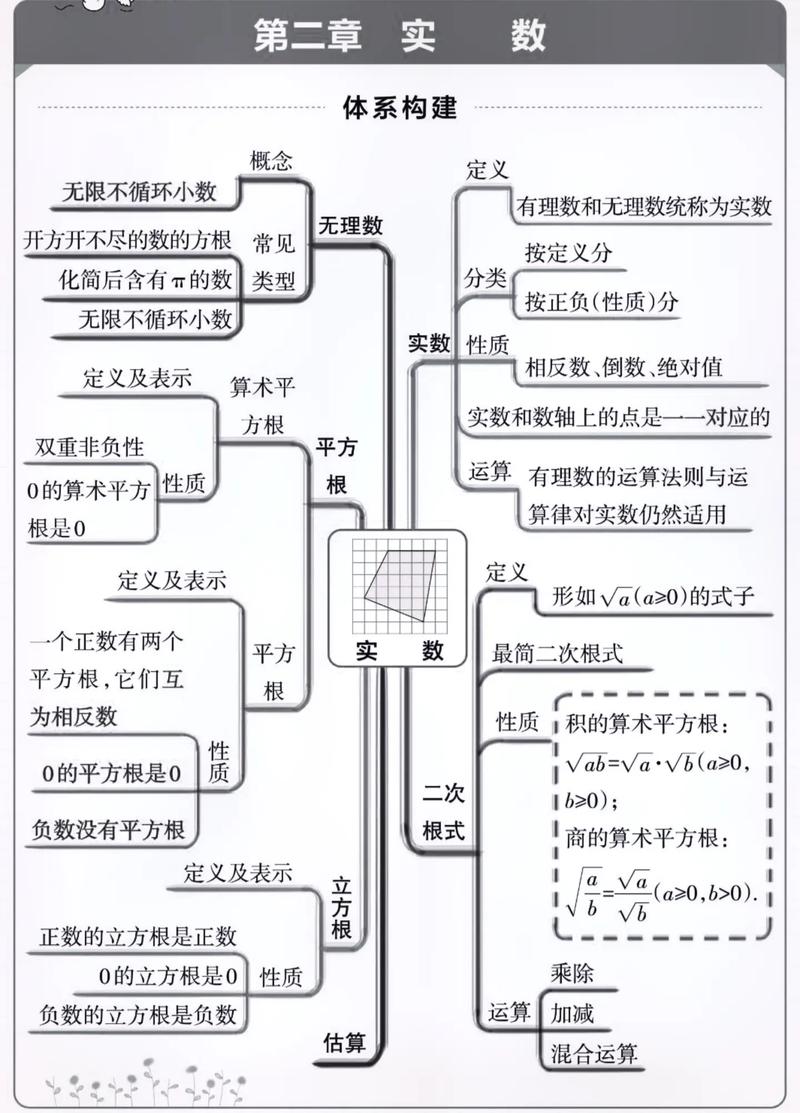
八年级上册数学第一单元核心知识点有哪些？

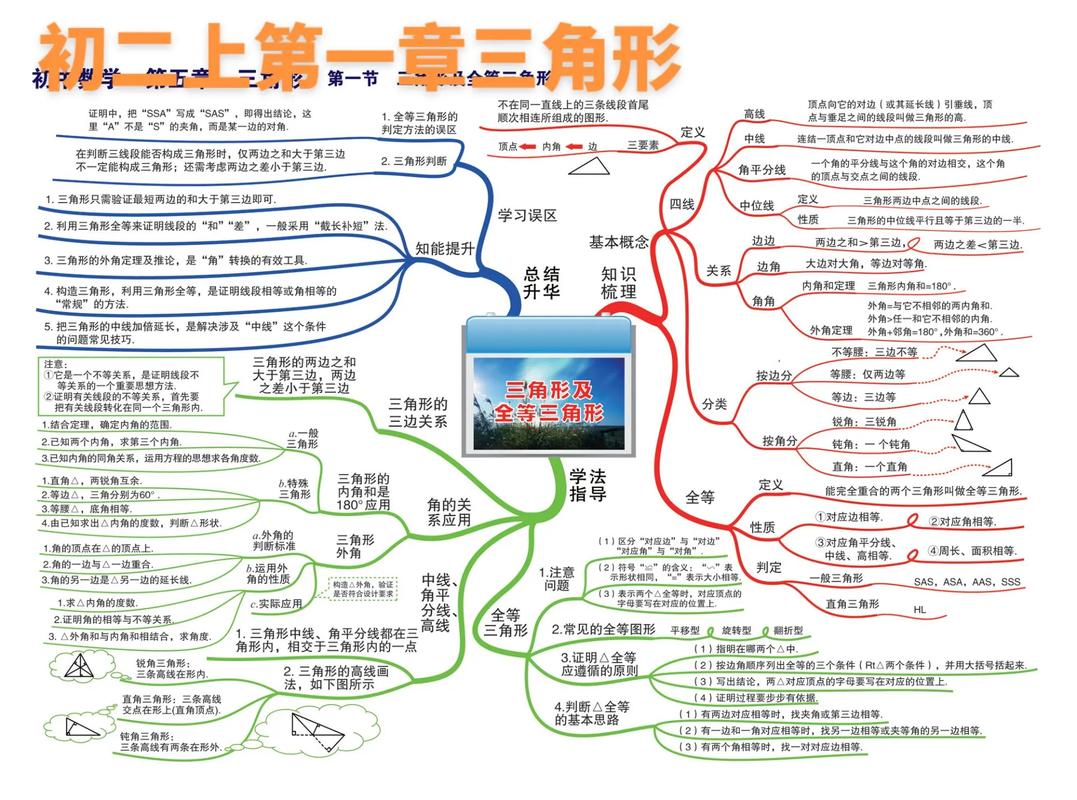
八年级上册数学第一单元：全等三角形

本单元是整个几何学习的基石，学好全等三角形对后续学习轴对称、勾股定理、四边形等内容至关重要。

---

核心概念

基本图形

• 三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形。
• 全等形：能够完全重合的两个图形。
• 全等三角形：能够完全重合的两个三角形。“完全重合”意味着它们的形状和大小都完全相同。

全等三角形的性质

全等三角形的对应元素相等。

• 对应边相等
• 对应角相等
• 对应边上的高、中线、角平分线分别相等
• 周长相等，面积相等

【要点】

• “对应”是关键：在描述全等三角形时，必须把对应顶点的字母写在对应的位置上。
  • 如果△ABC ≌ △DEF，
    • 点A对应点D，点B对应点E,点C对应点F。
    • 边AB对应边DE，边BC对应边EF,边AC对应边DF。
    • ∠A对应∠D，∠B对应∠E，∠C对应∠F。

---

判定全等三角形的方法

这是本单元的重中之重，是证明线段相等、角相等的主要工具。

判定方法	图形表示	关键点
边边边	三组对应边分别相等的两个三角形全等。	△ABC ≌ △DEF (AB=DE, AC=DF, BC=EF)	三边都对应相等，是证明全等的基础方法。
边角边	两边和它们的夹角对应相等的两个三角形全等。	△ABC ≌ △DEF (AB=DE, ∠B=∠E, BC=EF)	必须是“夹角”，即角必须是已知两边的夹角。
角边角	两角和它们的夹边对应相等的两个三角形全等。	△ABC ≌ △DEF (∠B=∠E, BC=EF, ∠C=∠F)	必须是“夹边”，即边必须是已知两角的公共边。
角角边	两角和其中一个角的对边对应相等的两个三角形全等。	△ABC ≌ △DEF (∠B=∠E, ∠C=∠F, AB=DE)	“AAS”是“ASA”的推论，因为已知两角，第三个角也相等。
斜边、直角边	斜边和一条直角边对应相等的两个直角三角形全等。	Rt△ABC ≌ Rt△DEF (∠C=∠F=90°, AB=DE, AC=DF)	仅适用于直角三角形，注意是“斜边”和“直角边”的对应。

【易错点与注意事项】

1. “SSA”或“ASS”不能判定全等：两边和其中一边的对角对应相等，不能保证两个三角形全等（可能会出现“边边角”的模糊情况）。
2. “AAA”不能判定全等：三个角对应相等只能保证两个三角形相似，不能保证全等（大小可能不同）。
3. 找准对应关系：在复杂的图形中，要善于通过公共边、公共角、对顶角等条件来寻找相等的边和角,从而确定对应关系。
4. 隐含条件：在证明全等时，不要忘记利用公共边、公共角、对顶角、等角（同角或等角的余角/补角）等隐含条件。

---

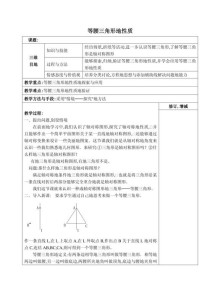
角平分线的性质

角平分线的定义

从一个角的顶点出发，把这个角分成两个相等的角的射线,叫做这个角的角平分线。

角平分线的性质定理

• 角平分线上的点到角的两边的距离相等。

• 图形语言：如图，OC是∠AOB的平分线，PD⊥OA，PE⊥OB，垂足分别是D、E，则 PD = PE。

      P
     / \
    /   \
   /     \
  D-------E
   \     /
    \   /
     \ /
      O-------A
           \
            \
             B

角平分线的判定定理

• 到一个角的两边的距离相等的点,在这个角的平分线上。
• 作用：可以用来证明角平分线。

---

学习建议与解题技巧

1. 打好基础：牢记全等三角形的五个判定方法,特别是它们的条件和适用范围。
2. 规范书写：证明过程要严谨，每一步都要有理有据，书写格式通常是：
   • “在△ABC和△△中”
   • “∵ (已知条件1)”
   • “∴ (由条件1得出的结论)”
   • “∵ (已知条件2或隐含条件)”
   • “∴ (由条件2得出的结论)”
   • “∴ △ABC ≌ △△ (判定方法，如SAS)”
   • “∴ (由全等得出的结论，如对应边相等、对应角相等)”
3. 学会“翻译”：将文字语言和图形语言“翻译”成数学符号语言。“点D是BC的中点”可以翻译成“BD = DC”。
4. 掌握基本模型：
   • “公共边”模型：两个三角形有公共边。
   • “公共角”模型：两个三角形有公共角。
   • “对顶角”模型：两个三角形有对顶角。
   • “角平分线+垂线”模型：利用角平分线性质证明线段相等。
5. 多加练习：通过做不同类型的题目，熟悉各种判定方法的应用场景,提高分析和解决问题的能力。

---

典型例题

例1：利用“SAS”证明全等 如图，已知AD∥BC，AD = CB，求证：△ADC ≌ △CBA。

证明： ∵ AD∥BC (已知) ∴ ∠DCA = ∠BAC (两直线平行，内错角相等) 在△ADC和△CBA中 { AD = CB (已知) ∠DCA = ∠BAC (已证) AC = CA (公共边) } ∴ △ADC ≌ △CBA (SAS)

例2：利用“AAS”证明全等 如图，AB⊥BD，ED⊥BD，垂足分别为B、D，且AB = CD，求证：∠A = ∠E。

分析：要证∠A = ∠E,可以证明它们所在的两个三角形全等。

证明： ∵ AB⊥BD，ED⊥BD (已知) ∴ ∠ABD = ∠EDC = 90° (垂直的定义) 在△ABD和△EDC中 { ∠ABD = ∠EDC (已证) ∠ADB = ∠EDC (对顶角相等) AB = CD (已知) } ∴ △ABD ≌ △EDC (AAS) ∴ ∠A = ∠E (全等三角形的对应角相等)

例3：利用角平分线性质 如图，在△ABC中，AD是∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，且AB = 8 cm，AC = 6 cm，求△DEF的周长。

解： ∵ AD是∠BAC的平分线 (已知) DE⊥AB，DF⊥AC (已知) ∴ DE = DF (角平分线上的点到角的两边的距离相等) 在△AED和△AFD中 { ∠EAD = ∠FAD (角平分线定义) ∠AED