八年级数学上册知识点总结有哪些重点？

八年级数学上册核心知识点总结

八年级数学上册的内容是整个初中数学的基石，特别是全等三角形和一次函数，是中考的重点和难点，学好这部分内容,对后续学习几何证明和函数思想至关重要。

---

第十一章 三角形

第一节 与三角形有关的线段

1. 三角形的边

   
   （图片来源网络，侵删）
   • 定义：由不在同一条直线上的三条线段首尾顺次相接所组成的图形。
   • 三边关系定理：三角形任意两边之和大于第三边，任意两边之差小于第三边。
   • 推论：已知三角形两边长度，第三边的长度范围是：两边之差 < 第三边 < 两边之和。

2. 三角形的高、中线、角平分线

   • 高：从一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段。

     特点：一个三角形有三条高，它们所在的直线交于一点（垂心）。

   • 中线：连接一个顶点和它对边中点的线段。

     特点：一个三角形有三条中线，它们交于一点（重心），且重心将中线分为 2:1 的两部分。

   • 角平分线：一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段。

     特点：一个三角形有三条角平分线，它们交于一点（内心）,内心是三角形内切圆的圆心。

     
     （图片来源网络，侵删）

3. 三角形的稳定性

   • 定义：三角形的三条边长确定后，其形状和大小就唯一确定了,这个性质叫做三角形的稳定性。
   • 应用：建筑、桥梁、自行车架等。

第二节 与三角形有关的角

1. 三角形的内角和

   • 定理：三角形的三个内角和等于 180°。

2. 三角形的外角

   • 定义：三角形的一边与另一边的延长线组成的角。
   • 外角定理：
     1. 三角形的一个外角等于与它不相邻的两个内角的和。
     2. 三角形的一个外角大于任何一个与它不相邻的内角。

---

第十二章 全等三角形

这是初中几何的核心章节,是学习几何证明的入门。

1. 全等三角形

   • 定义：能够完全重合的两个三角形叫做全等三角形。
   • 性质：全等三角形的对应边相等,对应角相等。

2. 判定三角形全等的方法

   • SSS (边边边)：三边对应相等的两个三角形全等。
   • SAS (边角边)：两边和它们的夹角对应相等的两个三角形全等。
   • ASA (角边角)：两角和它们的夹边对应相等的两个三角形全等。
   • AAS (角角边)：两角和其中一个角的对边对应相等的两个三角形全等。
   • HL (斜边、直角边)：斜边和一条直角边对应相等的两个直角三角形全等。（这是特殊方法）
   • 重要提醒：SSA 和 AAA 不能作为判定全等的依据。

3. 角平分线的性质

   • 性质定理：角平分线上的点到角两边的距离相等。
   • 判定定理：到一个角两边的距离相等的点,在这个角的平分线上。

---

第十三章 轴对称

本章从“形”的角度研究对称,为后续学习函数图像的对称性打下基础。

1. 轴对称

   • 定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形完全重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点,叫做对称点。
   • 性质：
     • 关于某条直线对称的两个图形是全等形。
     • 如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
     • 两个图形关于某条直线对称，如果它们的对应线段或延长线相交,那么交点在对称轴上。

2. 线段的垂直平分线

   • 性质：线段垂直平分线上的点与这条线段两个端点的距离相等。
   • 判定：与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。

3. 等腰三角形

   • 性质：
     • 两底角相等（等边对等角）。
     • 顶角平分线、底边上的中线、底边上的高互相重合（三线合一）。
   • 判定：有两个角相等的三角形是等腰三角形（等角对等边）。

4. 等边三角形

   • 性质：三个角都等于60°,三边都相等。
   • 判定：
     • 三个角都相等的三角形是等边三角形。
     • 有一个角是60°的等腰三角形是等边三角形。

5. 最短路径问题

   • 模型：在一条直线（对称轴）的同侧有两个点，如何在直线上找一点,使得到这两个点的距离之和最短？
   • 解法：作其中一个点关于这条直线的对称点，连接对称点和另一个点,与直线的交点即为所求。

---

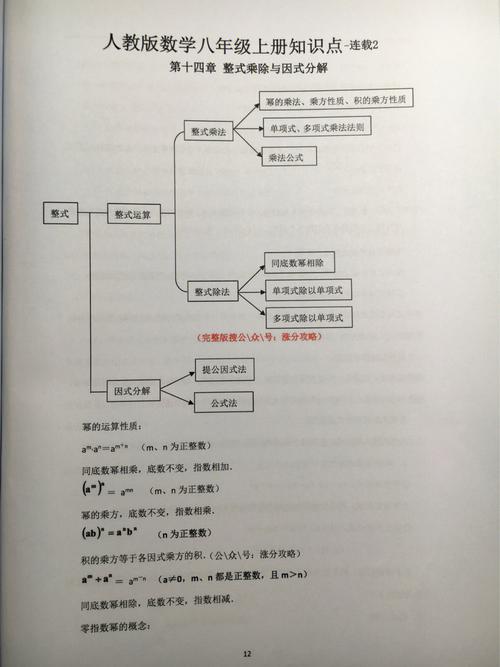
第十四章 整式的乘除与因式分解

本章是代数运算的核心,为解方程和函数学习提供工具。

第一节 整式的乘法

1. 幂的运算性质

   • 同底数幂相乘：a^m · a^n = a^(m+n)
   • 幂的乘方：(a^m)^n = a^(mn)
   • 积的乘方：(ab)^n = a^n · b^n
   • 同底数幂相除：a^m ÷ a^n = a^(m-n) (a ≠ 0)

2. 整式的乘法

   • 单项式 × 单项式：系数相乘，同底数幂相乘,其余字母连同它的指数不变作为积的因式。
   • 单项式 × 多项式：用单项式去乘多项式的每一项，再把所得的积相乘。（分配律）
   • 多项式 × 多项式：用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。（分配律）

3. 乘法公式

   • 平方差公式：(a+b)(a-b) = a² - b²
   • 完全平方公式：(a±b)² = a² ± 2ab + b²
   • 口诀：首平方，尾平方，中间两倍积（或差）,符号看中央。

第二节 整式的除法

1. 单项式 ÷ 单项式：系数相除，同底数幂相除，只在被除式里出现的字母,连同它的指数作为商的一个因式。
2. 多项式 ÷ 单项式：把这个多项式的每一项除以这个单项式，再把所得的商相加。（分配律）

第三节 因式分解

1. 定义：把一个多项式化为几个整式的积的形式。
2. 常用方法
   • 提公因式法：ma + mb + mc = m(a+b+c)
   • 公式法：
     • 平方差公式：a² - b² = (a+b)(a-b)
     • 完全平方公式：a² ± 2ab + b² = (a±b)²
   • 十字相乘法：用于二次三项式 ax²+bx+c 的因式分解。
3. 因式分解的一般步骤：一提（公因式）、二套（公式）、三分组（十字相乘）、四彻底（检查是否还能继续分解）。

---

第十五章 分式

本章是分数的“升级版”,其性质和运算法则与分数高度相似。

1. 分式的定义与基本性质

   • 定义：形如 A/B（A、B是整式，B中含有字母且B≠0）的式子叫做分式。
   • 基本性质：分式的分子与分母同乘（或除以）一个不等于0的整式，分式的值不变。
     • A/B = (A·M) / (B·M) (M≠0)
     • A/B = (A÷M) / (B÷M) (M≠0)

2. 分式的运算

   • 约分与通分：分式运算的基础,依据是分式的基本性质。
   • 加减法：同分母分式相加减，分母不变，把分子相加减；异分母分式相加减，先通分，变为同分母分式,再加减。
   • 乘除法：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母；分式除以分式，把除式的分子、分母颠倒位置后,与被除式相乘。
   • 乘方：分式的乘方是把分子、分母分别乘方。(A/B)^n = A^n / B^n

3. 整数指数幂

   • 零指数幂：a⁰ = 1 (a≠0)
   • 负整数指数幂：a⁻ⁿ = 1/aⁿ (a≠0, n为正整数)
   • 拓展了幂的运算性质：如 a^m · a^n = a^(m+n) 在m,n为整数时也成立。

4. 分式方程

   • 定义：分母中含有未知数的方程。
   • 解法步骤：
     1. 在方程两边同乘最简公分母，约去分母,化为整式方程。
     2. 解这个整式方程。
     3. 验根：把整式方程的根代入最简公分母，若不为0，则是原方程的根；若为0，则是增根,必须舍去。
   • 应用：列分式方程解应用题（如行程问题、工程问题）。

---

第十六章 二次根式

本章是数与式的延伸,为后续学习一元二次方程和二次函数做准备。

1. 二次根式的概念

   • 定义：式子 √a (a≥0) 叫做二次根式。
   • 被开方数的非负性：a ≥ 0。

2. 二次根式的性质

   • 基本性质：(√a)² = a (a≥0)
   • 性质二：√(a²) = |a| = { a (a≥0), -a (a<0) }
   • 性质三（乘法法则）：√a · √b = √(ab) (a≥0, b≥0)
   • 性质四（除法法则）：√a / √b = √(a/b) (a≥0, b>0)

3. 二次根式的加减

   • 定义：几个二次根式化成最简二次根式后，如果被开方数相同,这几个二次根式就叫做同类二次根式。
   • 方法：先化成最简二次根式，再合并同类二次根式（类似于合并同类项）。

4. 二次根式的混合运算

   • 运算顺序：先算乘方，再算乘除，最后算加减,有括号的先算括号里的。
   • 运算律：交换律、结合律、分配律同样适用。
   • 分母有理化：化去分母中的根号，常用方法：分子分母同乘分母的有理化因式（如 √a 的有理化因式是 √a，a+√b 的有理化因式是 a-√b）。

---

第十七章 一次函数

本章是初中函数的入门，是数形结合思想的集中体现,是中考的重中之重。

1. 变量与函数

   • 常量与变量：在变化过程中，数值发生变化的量是变量,数值保持不变的量是常量。
   • 函数的定义：在一个变化过程中，有两个变量 x 和 y，如果对于 x 的每一个确定的值，y 都有唯一确定的值与其对应，那么就说 y 是 x 的函数，x 是自变量，y 是因变量。
   • 自变量的取值范围：
     • 整式：全体实数。
     • 分式：分母不为0。
     • 二次根式：被开方数≥0。
     • 实际问题：要使实际问题有意义。
   • 函数的表示方法：解析法、列表法、图像法。

2. 正比例函数

   • 定义：形如 y = kx (k≠0) 的函数。
   • 图像：经过原点 (0, 0) 的一条直线。
   • 性质：
     • 当 k > 0 时，图像经过一、三象限,y随x的增大而增大。
     • 当 k < 0 时，图像经过二、四象限,y随x的增大而减小。

3. 一次函数

   • 定义：形如 y = kx + b (k≠0) 的函数，当 b=0 时,它就是正比例函数。
   • 图像：一条直线，可以看作是由正比例函数 y=kx 的图像平移 |b| 个单位长度得到（当 b>0 时，向上平移；当 b<0 时，向下平移）。
   • 性质：
     • 当 k > 0 时，y随x的增大而增大；当 k < 0 时,y随x的增大而减小。
     • 图像与y轴的交点坐标是 (0, b),b也叫截距。
     • 图像与x轴的交点坐标是 (-b/k, 0)。
   • 待定系数法求解析式：知道图像上任意两点的坐标，可以列出关于 k 和 b 的二元一次方程组,解方程组即可求出解析式。

4. 一次函数与方程（组）、不等式的关系

   • 一次函数与一元一次方程：一次函数 y=kx+b 的图像与x轴交点的横坐标就是方程 kx+b=0 的解。
   • 一次函数与二元一次方程组：两个一次函数图像的交点坐标就是由这两个函数解析式组成的方程组的解。
   • 一次函数与一元一次不等式：
     • 不等式 kx+b > 0 的解集是函数图像在x轴上方部分对应的x的取值范围。
     • 不等式 kx+b < 0 的解集是函数图像在x轴下方部分对应的x的取值范围。

---

复习建议

1. 回归课本：确保所有定义、定理、公式、性质都准确无误地理解和记忆。
2. 整理笔记：将每个章节的知识点、典型例题、易错点整理成自己的笔记,形成知识网络。
3. 多做练习：特别是几何证明题和函数综合题，通过练习来巩固方法,提高解题速度和准确率。
4. 建立错题本：将做错的题目抄录下来，分析错误原因（是概念不清、计算失误还是思路错误），定期回顾,避免再犯。
5. 数形结合：在学习函数和几何时，一定要养成画图的习惯，利用图形直观地理解问题、解决问题。

希望这份总结能对你的学习有所帮助！加油！