九年级数学二次函数应用题怎么解?
校园之窗 2025年12月11日 20:58:33 99ANYc3cd6
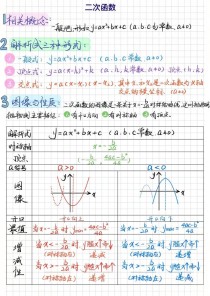
核心知识点回顾
- 二次函数的一般形式:
y = ax² + bx + c(a ≠ 0) - 二次函数的顶点式:
y = a(x - h)² + k- 顶点坐标为 (h, k)
- 对称轴为直线 x = h
- 二次函数的交点式:
y = a(x - x₁)(x - x₂)- 与x轴的交点坐标为 (x₁, 0) 和 (x₂, 0)
- 二次函数的性质:
- 开口方向: 由
a的符号决定。a > 0,开口向上,有最小值。a < 0,开口向下,有最大值。
- 最值问题: 顶点坐标的纵坐标
k就是函数的最大值或最小值。 - 对称性: 关于对称轴
x = h对称。
- 开口方向: 由
常见应用题题型及解题步骤
解题通用步骤:
- 审题: 仔细阅读题目,理解题意,找出关键量(自变量和因变量)。
- 设元: 设出自变量
x和因变量y。 - 建模: 根据题目中的等量关系,列出
y与x之间的函数关系式(二次函数)。 - 求解: 根据题目要求,利用二次函数的性质(如顶点、对称轴、与坐标轴的交点等)进行计算或分析。
- 检验: 检验求得的解是否符合实际意义(如边长、高度、时间等必须为正数)。
- 作答: 写出完整的答案。
利润最大问题
这是最经典的应用题类型,通常涉及商品的单价、销量、总成本、总利润等。
核心关系式:

- 总利润 = (单件售价 - 单件成本) × 销售量
- 总利润 = 销售额 - 总成本
解题关键: 找出“利润”与“销售量”或“售价”之间的二次函数关系,然后求其最大值。
几何图形最值问题
通常涉及矩形的面积、周长,或者几何体(如圆柱、圆锥)的表面积、体积等。
核心关系式:
- 矩形面积 = 长 × 宽
- 圆柱体积 = 底面积 × 高
- 圆柱侧面积 = 底面周长 × 高
解题关键: 利用几何图形的内在联系(如相似三角形、勾股定理、固定周长等)建立变量关系,将面积或体积表示为某个变量的二次函数,然后求其最大值或最小值。

抛物线运动问题(物理应用)
通常描述物体(如小球、炮弹)的斜抛运动,其轨迹是一条抛物线。
核心关系式:
- 高度 h 与水平距离 x 的关系:
h = ax² + bx + c - 最高点: 抛物线的顶点,对应最大高度。
- 落地: 当
h = 0时,求出的x值就是物体的水平射程。
解题关键: 理解 a, b, c 的物理意义(如 c 通常是初始高度),利用顶点式求解最高点和对称轴。
典型例题精讲
例题1:利润最大化问题
某商店购进一种商品,进价为每件20元,市场调查发现,如果以每件30元销售,每天可卖出100件;在此基础上,销售单价每提高1元,每天的销售量就减少5件,设销售单价为 x 元,每天的利润为 w 元。

(1) 求 w 与 x 之间的函数关系式;
(2) 当销售单价定为多少元时,每天的利润最大?最大利润是多少?
解析:
(1) 求函数关系式
- 设元: 设销售单价为
x元,每天的利润为w元。 - 找关系:
- 单件利润 = 销售价 - 进价 =
(x - 20)元。 - 销售量: 基础销售量为100件,每提价1元,销量减5件,提价了
(x - 30)元,所以销量减少了5(x - 30)件。- 实际销售量 =
100 - 5(x - 30) = 100 - 5x + 150 = 250 - 5x件。
- 实际销售量 =
- 单件利润 = 销售价 - 进价 =
- 建模: 利润 = 单件利润 × 销售量
w = (x - 20)(250 - 5x)w = -5x² + 250x + 100x - 5000w = -5x² + 350x - 5000注意:这个二次函数开口向下,有最大值。
(2) 求最大利润
方法一:配方法(化为顶点式)
w = -5(x² - 70x) - 5000
w = -5(x² - 70x + 35² - 35²) - 5000
w = -5[(x - 35)² - 1225] - 5000
w = -5(x - 35)² + 6125 - 5000
w = -5(x - 35)² + 1125
- 顶点坐标为
(35, 1125)。 - 因为
a = -5 < 0,所以当x = 35时,w有最大值,最大利润是1125元。
公式法(利用顶点横坐标公式 x = -b/2a)
a = -5,b = 350- 顶点的横坐标
x = -b / (2a) = -350 / (2 × -5) = 350 / 10 = 35 - 将
x = 35代入原函数求w:w = (35 - 20)(250 - 5 × 35) = 15 × (250 - 175) = 15 × 75 = 1125元。
答案:
(1) w = -5x² + 350x - 5000
(2) 当销售单价定为35元时,每天的利润最大,最大利润是1125元。
例题2:几何图形最值问题
如图,用长为60米的篱笆靠墙围成一个矩形花园(墙足够长),设矩形的一边长为 x 米。
(1) 求花园面积 S 与 x 之间的函数关系式;
(2) 当 x 为多少时,花园的面积最大?最大面积是多少?
解析:
- 分析: 篱笆总长为60米,用于围三条边(两条宽和一条长,或两条长和一条宽),我们需要根据
x的定义来确定哪一边是x。- 情况一: 假设
x是与墙平行的边的长度。- 则另外两条与墙垂直的边长度之和为
(60 - x)米,每条边长为(60 - x) / 2米。 - 面积
S = x × (60 - x) / 2 = -0.5x² + 30x。
- 则另外两条与墙垂直的边长度之和为
- 情况二: 假设
x是与墙垂直的边的长度。- 则与墙平行的边长为
(60 - 2x)米。 - 面积
S = x × (60 - 2x) = -2x² + 60x。
- 则与墙平行的边长为
- 通常题目会给出示意图或明确说明,我们以情况二为例进行解答。
- 情况一: 假设
(1) 求函数关系式
- 设与墙垂直的边长为
x米,则与墙平行的边长为(60 - 2x)米。 - 面积
S = x(60 - 2x) = -2x² + 60x。 - 注意自变量
x的取值范围: 边长必须为正数。x > 060 - 2x > 0=>x < 300 < x < 30。
(2) 求最大面积
S = -2x² + 60x是一个开口向下的抛物线,有最大值。- 顶点横坐标
x = -b / (2a) = -60 / (2 × -2) = 60 / 4 = 15。 x = 15在其取值范围(0, 30)内。- 将
x = 15代入函数求S:S = -2(15)² + 60(15) = -2 × 225 + 900 = -450 + 900 = 450平方米。
答案:
(1) S = -2x² + 60x (0 < x < 30)
(2) 当与墙垂直的边长为15米时,花园的面积最大,最大面积是450平方米。
解题技巧与注意事项
- 定义域是关键: 二次函数的图像是无限延伸的,但实际问题中的自变量(如长度、时间、价格)都有其取值范围。求出的解必须在定义域内才有效。
- 选择合适的函数形式:
- 求最值问题,顶点式最方便。
- 已知与x轴的交点(如求落地时间、盈利与亏损的平衡点),交点式最方便。
- 一般情况,一般式是基础。
- 理解
a的作用:a的符号决定了开口方向,从而决定了函数有最大值还是最小值,这是判断“最大利润”还是“最小成本”的第一步。 - 建立模型是核心: 将文字语言转化为数学符号和关系式是解题中最难的一步,一定要反复读题,找出等量关系。
- 注意单位: 最后作答时,不要忘记带上单位(如元、平方米、秒等)。
希望这份详细的总结能帮助你攻克九年级二次函数应用题!多加练习,掌握建模的思路,你会发现这类题目其实有很强的规律性,祝你学习进步!