人教版八年级上册数学期末试题难度如何？

校园之窗 2025年11月30日 19:19:09 99ANYc3cd6 1 0

人教版八年级上册数学期末模拟试题

考试时间： 120分钟 满分： 120分

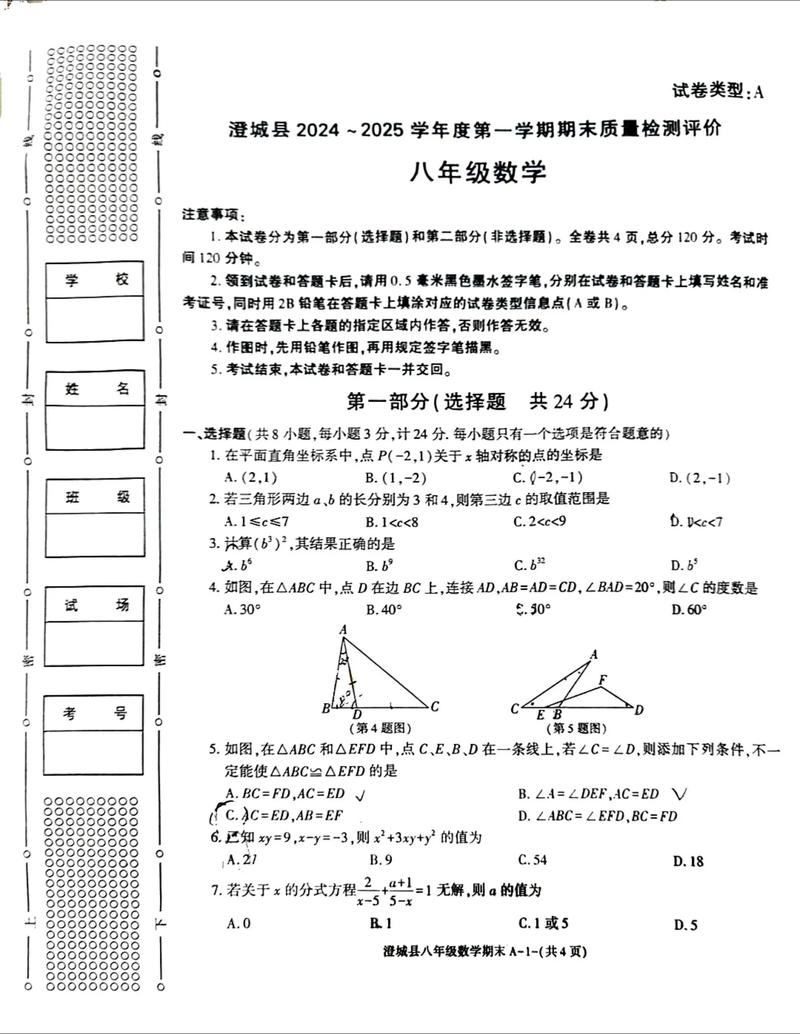
选择题（每小题3分，共30分）

下列实数中,是无理数的是 A. 0 B. -2 C. √8 D. 1/3
（图片来源网络，侵删）
下列计算正确的是 A. a² + a³ = a⁵ B. (a²)³ = a⁵ C. a⁶ ÷ a² = a³ D. (2a)² = 4a²
下列各式从左到右的变形中,是因式分解的是 A. x² - 4 = (x + 2)(x - 2) B. (x + 2)(x - 2) = x² - 4 C. x² - 4 + 3x = (x + 2)(x - 2) + 3x D. x² - 4 = (x + 2)² - 4x
一次函数 y = -2x + 3 的图象不经过 A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
下列命题中,是真命题的是 A. 两条直线被第三条直线所截，同位角相等 B. 有两条边和一个角对应相等的两个三角形全等 C. 两条直线相交，只有一个交点 D. 任何数的平方都是正数
（图片来源网络，侵删）
若等腰三角形的一个角为50°，则它的顶角的度数为 A. 50° B. 80° C. 50°或80° D. 无法确定
若点 A(1, y₁) 和 B(2, y₂) 都在直线 y = -x + 3 上，则 y₁ 与 y₂ 的大小关系是 A. y₁ > y₂ B. y₁ < y₂ C. y₁ = y₂ D. 无法确定
一个多边形的内角和是它的外角和的2倍,则这个多边形是 A. 三角形 B. 四边形 C. 五边形 D. 六边形
如图,在△ABC中，∠C = 90°，AB的垂直平分线交BC于点D，交AB于点E，连接AD，若∠B = 30°，则∠CAD的度数为
（图片来源网络，侵删）

(此处应有图形：一个直角三角形ABC，∠C=90°，AB是斜边，DE是AB的垂直平分线，D在BC上，E在AB上。) A. 30° B. 45° C. 60° D. 75°
小明从家出发步行去图书馆,去时以每分钟60米的速度行走，用了15分钟到达；在图书馆待了一段时间后，原路返回，以每分钟80米的速度行走，设小明从家出发后所用时间为x分钟，离家的距离为y米，则下列能大致反映y与x之间函数关系的图象是

(此处应有四个函数图象选项) A. 一个折线图，先上升，水平，再下降。 B. 一个折线图，先上升，再下降。 C. 一条直线。 D. 一个折线图，先上升，水平，再上升。

填空题（每小题3分，共24分）

4的平方根是 ____。
计算：(-2a²b)³ = ____。
因式分解：mx² - 4m = ____。
点P(-3, 5)关于y轴对称的点的坐标是 ____。
已知一次函数 y = (m-1)x + m² - 1 的图象经过原点，则m的值为 ____。
如图,在△ABC中，∠B = ∠C，点D、E分别在边AB、AC上，且AD = AE，请添加一个条件，使得△ABE ≅ △ACD，你添加的条件是 ____（只需写出一个）。

(此处应有图形：一个等腰三角形ABC，AB=AC，D在AB上，E在AC上，AD=AE。) (答案不唯一，如：∠B = ∠C 或 AB = AC 或 ∠AEB = ∠ADC)
一个等腰三角形的一边长为5,另一边长为10，则其周长为 ____。
已知a、b满足方程组 { 2x + y = 5 }，则代数式 (x-y)(x+y) 的值为 ____。 { x - y = 1 }

解答题（共66分）

(本题8分) 计算： (1) √18 + (√2 - 1)⁰ - |1 - √3| (2) (2a + b)² - (2a - b)(2a + b)
(本题8分) 因式分解： (1) a³ - 4a (2) 4x² - 4xy + y² - z²
(本题8分) 如图，在△ABC中，AD是BC边上的高，BE是AC边上的中线，AD与BE交于点F，已知AB = AC。

(此处应有图形：一个等腰三角形ABC，AB=AC，AD是高，BE是中线，交于F。) 求证：△ABD ≅ △ACD。
(本题10分) 为了响应“绿色出行”的号召，某市计划开通A、B两条共享单车线路，线路A的收费标准是：起步价3元（30分钟内含），超过30分钟后，每分钟0.2元；线路B的收费标准是：起步价2元（30分钟内含），超过30分钟后，每分钟0.3元。 (1) 分别写出乘坐线路A、B的租车费用y（元）与租车时间x（x > 30，单位：分钟）之间的函数关系式。 (2) 如果小明想租一辆单车骑行45分钟，选择哪条线路更划算？
(本题10分) 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(-1, 2)，B(3, 1)，C(1, -2)。

(此处应有平面直角坐标系，并标出A、B、C三点) (1) 画出△ABC关于y轴对称的△A₁B₁C₁。 (2) 写出点A₁、B₁、C₁的坐标。 (3) 求△ABC的面积。
(本题12分) 如图，在△ABC中，∠ACB = 90°，AC = BC，D是AB的中点，过点D作DE⊥AC，垂足为E。

(此处应有图形：一个等腰直角三角形ABC，∠C=90°，AC=BC，D是AB中点，DE⊥AC于E。) (1) 求证：△ADE ≌ △BDC。 (2) 若AB = 10 cm，求线段DE的长度。
(本题10分) 阅读理解：我们定义：如果一个三角形的一边长为a，这边上的高为h，那么这个三角形的面积 S = 1/2 a h，如果一个三角形的三边长分别为a, b, c，其面积S也可以用海伦公式计算：S = √[p(p-a)(p-b)(p-c)]，p = (a+b+c)/2。

问题：在△ABC中，已知AB = 5，BC = 6，AC = 7。 (1) 请用两种方法计算△ABC的面积。（要求：一种用底乘以高除以二，另一种用海伦公式） (2) 求△ABC的AC边上的高BD的长度。