九年级反比例函数重点难点如何突破？
校园之窗 2025年12月17日 18:45:32 99ANYc3cd6
人教版九年级数学 - 反比例函数 知识点详解
核心概念
定义
一般地，形如 y = k/x (k为常数，k ≠ 0) 的函数,称为反比例函数。
- 自变量：
x - 因变量：
y - 比例系数：
k(k是一个不等于0的常数) - 定义域：因为分母不能为0，所以自变量
x的取值范围是x ≠ 0。
注意事项
（图片来源网络，侵删）
- 反比例函数也可以写成
y = kx⁻¹的形式。 - 函数解析式中的
k是一个常数，不能含有x或y。y = 2/x是反比例函数，而y = x/2是正比例函数，y = 2/x + 1不是反比例函数。 k的符号（正或负）决定了函数图像所在的象限和函数的增减性。
图像与性质
图像 反比例函数的图像是双曲线，它有两个分支，并且这两个分支关于原点对称。
图像的位置与 k 的关系
-
当
k > 0时：- 图像位于第一、三象限。
- 在每个象限内，
y随x的增大而减小（减函数）。 - 如图所示：
-
当
k < 0时：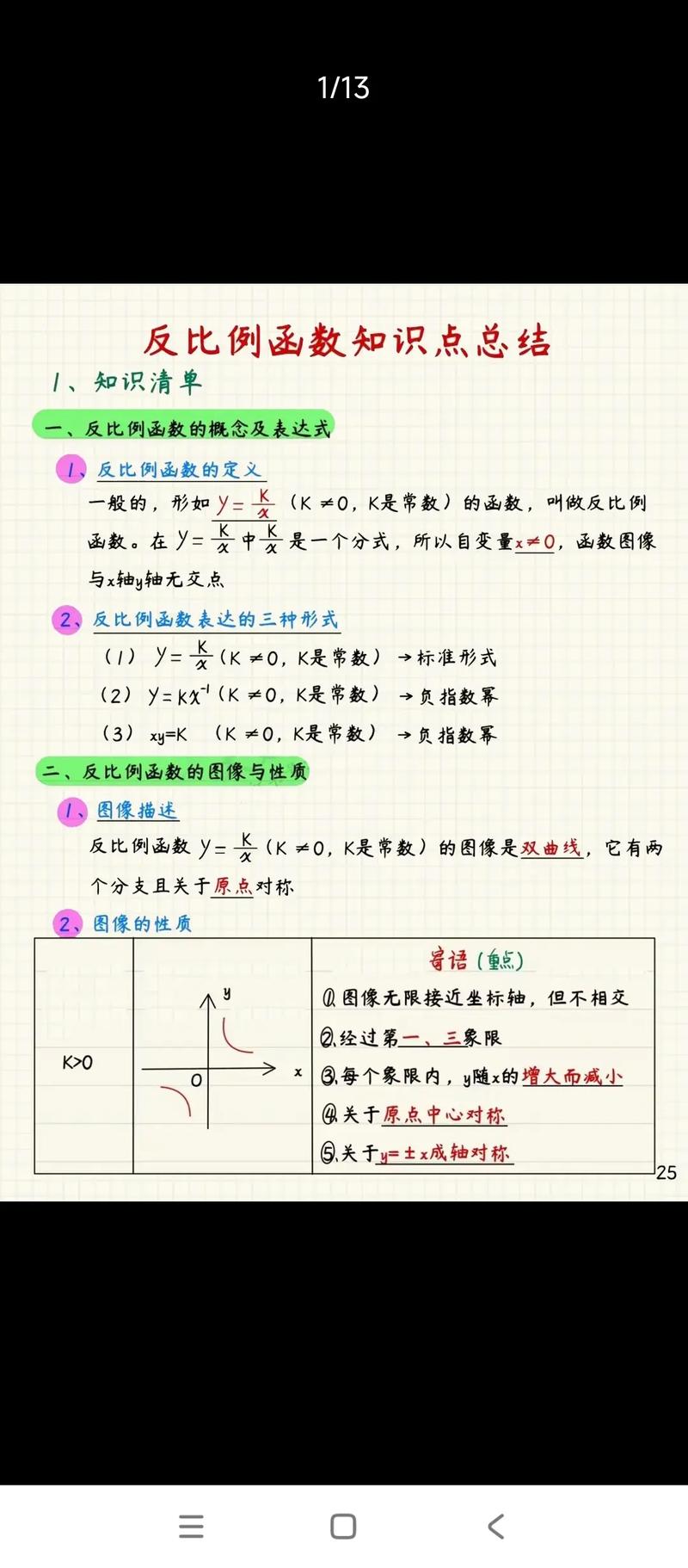
（图片来源网络，侵删）- 图像位于第二、四象限。
- 在每个象限内，
y随x的增大而增大（增函数）。 - 如图所示：
重要性质
- 对称性：
- 图像关于原点成中心对称。
- 图像关于直线
y = x和 直线y = -x成轴对称。
- 渐近线：
- 图像无限接近于坐标轴，但永远不会与坐标轴相交。
x轴（即y = 0）是图像的一条水平渐近线。y轴（即x = 0）是图像的一条垂直渐近线。
- 增减性：
- 必须强调“在每个象限内”。
- 不能说“当
k > 0时，函数值y随x的增大而减小”，因为当x从第一象限的负值变到第三象限的负值时，y是从负值变为正值,是增大的。
重要考点与题型
确定反比例函数解析式
- 核心：求出比例系数
k。 - 方法：将图像上任意一点
(x, y)的坐标代入y = k/x，求出k的值。 - 例题：反比例函数的图像经过点
(2, 3)，求这个函数的解析式。- 解：将
(2, 3)代入y = k/x，得3 = k/2，解得k = 6。 - 函数解析式为
y = 6/x。
- 解：将
比较函数值的大小
- 核心：根据
k的符号和点所在的象限进行比较。 - 方法：
- 先确定
k的符号,判断图像所在的象限。 - 比较点的横坐标
x的大小。 - 根据“在每个象限内，
y随x的变化规律”进行比较。
- 先确定
- 例题：已知点
A(x₁, y₁)和B(x₂, y₂)都在反比例函数y = -4/x的图像上，且x₁ > x₂ > 0，比较y₁和y₂的大小。- 解：因为
k = -4 < 0，所以图像在第二、四象限。 - 因为
x₁ > x₂ > 0，所以点A和B都在第四象限。 - 在第四象限内，
y随x的增大而增大。 - 因为
x₁ > x₂，y₁ > y₂。
- 解：因为
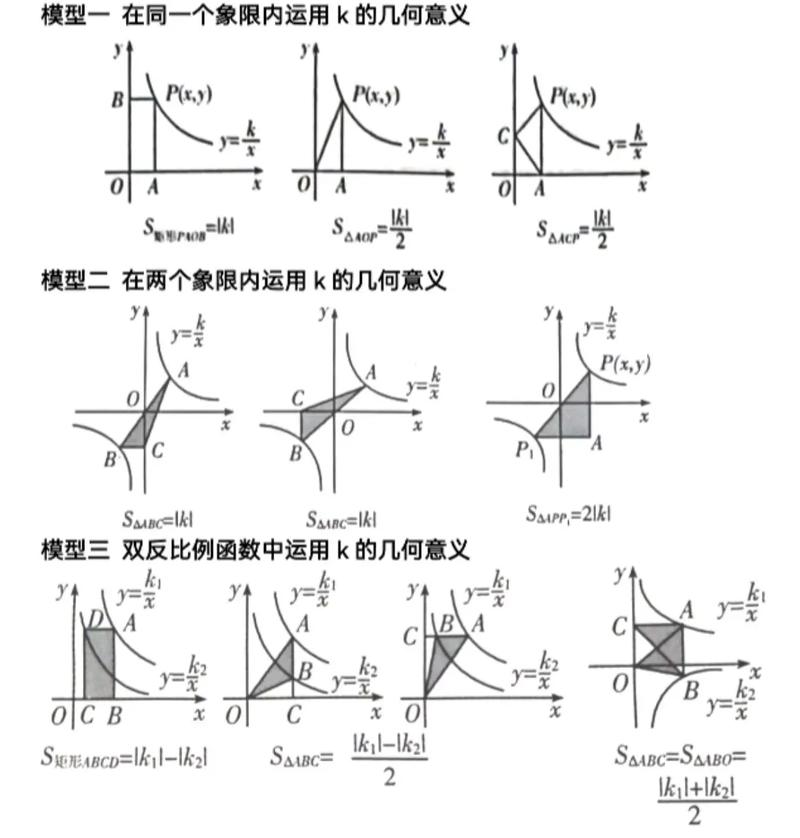
与几何图形结合（面积问题）
（图片来源网络，侵删）
- 核心性质：过反比例函数图像上任意一点
P(a, b)作x轴、y轴的垂线，所得矩形的面积为S = |a| * |b|。- 因为点
P(a, b)在图像上，b = k/a，即ab = k。 - 矩形的面积
S = |ab| = |k|。
- 因为点
- 过反比例函数图像上任意一点作坐标轴的垂线，与坐标轴围成的矩形的面积等于
|k|,是一个定值。 - 推广：
- 连接该点与原点，所得三角形的面积为
S = (1/2) * |ab| = (1/2) * |k|,也是一个定值。 - 由该点、原点以及垂足构成的直角三角形的面积也是
(1/2) * |k|。
- 连接该点与原点，所得三角形的面积为
与一次函数的交点问题
- 核心：求两个函数图像的交点坐标,就是解由它们的解析式组成的方程组。
- 方法：联立方程组，解出
(x, y)即为交点坐标。 - 例题：反比例函数
y = 6/x与一次函数y = x + 5有交点吗？若有，求出交点坐标。- 解：联立方程组：
y = 6/xy = x + 5 - 将第二个等式代入第一个，得
x + 5 = 6/x。 - 整理得
x² + 5x - 6 = 0。 - 因式分解
(x + 6)(x - 1) = 0。 - 解得
x₁ = -6，x₂ = 1。 - 当
x = -6时，y = -6 + 5 = -1。 - 当
x = 1时，y = 1 + 5 = 6。 - 两个交点坐标分别为
(-6, -1)和(1, 6)。
- 解：联立方程组：
- 图像特点：反比例函数和一次函数的图像通常有两个交点（当联立后的一元二次方程判别式大于0时），一个在第一象限，一个在第三象限（当
k>0且一次函数y=kx+b中b>0时）。
易错点提醒
- 忽略定义域：忘记
x ≠ 0的条件。 - 混淆增减性：忘记“在每个象限内”这个前提,错误地跨象限比较。
- 面积计算错误：忘记面积是
|k|，而不是k，当k为负数时,面积不能为负。 - 交点个数判断错误：认为反比例函数和一次函数一定有两个交点，实际上可能没有交点（联立后方程无实数解）或只有一个交点（相切）。
k的几何意义：混淆k的值与图像围成的面积。S_矩形 = |k|，S_三角形 = (1/2)|k|。
学习方法建议
- 数形结合：这是学习函数最重要的方法，看到一个解析式，要能立刻想到它的图像形状和位置；看到一个双曲线，要能立刻想到它的解析式
k的符号。 - 列表描点：对于不熟悉的函数，可以通过列表、描点、连线的方式自己画一次图像,加深对性质的理解。
- 对比学习：将反比例函数与之前学过的正比例函数、一次函数进行对比，理解它们的区别和联系（如
y=kxvsy=k/x）。 - 多做练习：特别是几何综合题,熟练掌握面积问题的解法。
希望这份详细的梳理能帮助你更好地掌握反比例函数！祝你学习进步！
