北师大版八年级下册数学书重点难点是什么？

教材基本信息

• 出版社： 北京师范大学出版社
• 全称： 《义务教育教科书·数学 八年级下册》
• 主编： 马复、王申怀
• 本册书主要围绕图形的变换、一次函数和数据的分析三大核心板块展开，同时包含重要的证明内容，是初中数学承上启下的关键一册。

---

各章节核心知识点详解

本册书通常包含以下章节：

第一章 三角形的证明

这是本册书的几何基础,也是对七年级几何知识的深化和系统化，引入了严格的逻辑证明。

1. 等腰三角形

   • 性质与判定：
     • 性质： 等边对等角；三线合一（顶角平分线、底边上的中线、底边上的高线互相重合）。
     • 判定： 等角对等边。
   • 证明： 学习用“因为.....”的形式，结合全等三角形（SSS, SAS, ASA, AAS）等知识，严格证明等腰三角形的性质和判定。

2. 直角三角形

   • 性质：
     • 两个锐角互余。
     • 勾股定理： 如果直角三角形的两直角边长为 a, b，斜边长为 c，a² + b² = c²，这是几何中最重要的定理之一。
     • 勾股定理的逆定理： 如果三角形的三边长 a, b, c 满足 a² + b² = c²，那么这个三角形是直角三角形。
   • 证明： 证明勾股定理及其逆定理，并解决实际问题（如距离计算）。

3. 线段的垂直平分线与角平分线

   • 线段垂直平分线：
     • 性质： 线段垂直平分线上的点到线段两端点的距离相等。
     • 判定： 到线段两端点距离相等的点，在这条线段的垂直平分线上。
   • 角平分线：
     • 性质： 角平分线上的点到角的两边的距离相等。
     • 判定： 到角的两边距离相等的点，在这个角的平分线上。
   • 证明： 证明上述性质和判定，并理解它们的应用。

4. 互逆命题与互逆定理

   
   （图片来源网络，侵删）
   • 概念： 交换一个命题的题设和结论，所得到的命题就是原命题的逆命题。
   • 关系： 原命题成立，其逆命题不一定成立，如果原命题和逆命题都成立，那么它们就互为逆定理（如勾股定理及其逆定理）。

第二章 一元一次不等式与一元一次不等式组

这是代数部分的重要内容,是对之前一元一次方程学习的延伸和拓展。

1. 不等式的基本性质

   • 性质1： 不等式两边加（或减）同一个数（或式子），不等号的方向不变。
   • 性质2： 不等式两边乘（或除以）同一个正数，不等号的方向不变。
   • 性质3： 不等式两边乘（或除以）同一个负数，不等号的方向改变。（这是最容易出错的地方！）

2. 一元一次不等式

   • 定义： 含有一个未知数，未知数的次数是1的不等式。
   • 解法： 与解一元一次方程类似，但要注意性质3的应用。
   • 解集： 不等式所有解的集合。
   • 数轴表示： 在数轴上直观地表示解集，空心圈表示不包含该点，实心点表示包含该点。

3. 一元一次不等式组

   
   （图片来源网络，侵删）
   • 定义： 含有相同未知数的几个一元一次不等式合在一起。
   • 解法： 分别求出每个不等式的解集，再求它们的公共部分（交集）。
   • 解集的确定： 利用口诀“同大取大，同小取小，大小小大中间找，大大小小无解了”。
   • 应用： 解决实际问题，如方案选择、最优化问题等。

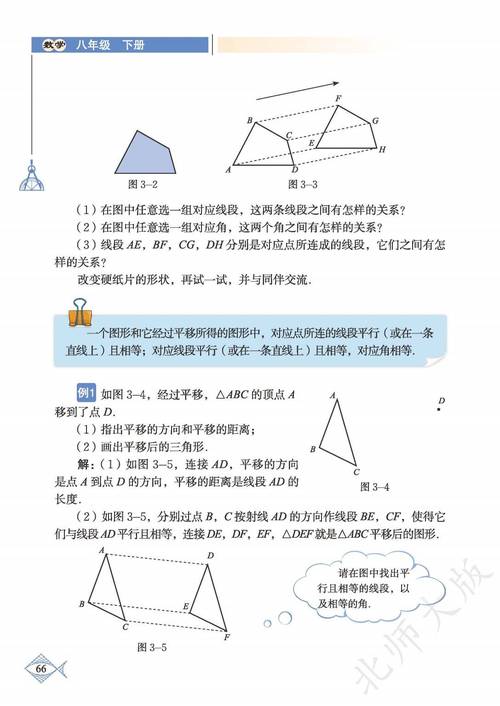
第三章 图形的平移与旋转

本章是图形变换的核心,培养学生的空间想象能力和几何直观。

1. 平移

   • 定义： 在平面内，将一个图形沿某个方向移动一定的距离，这种图形运动称为平移。
   • 性质：
     • 平移不改变图形的形状和大小。
     • 连接各组对应点的线段平行（或在同一直线上）且相等。
   • 作图： 确定平移的方向和距离，找出关键点的对应点，连接成新图形。

2. 旋转

   • 定义： 在平面内，将一个图形绕一个定点（旋转中心）沿某个方向转动一个角度，这种图形运动称为旋转。
   • 性质：
     • 旋转不改变图形的形状和大小。
     • 对应点到旋转中心的距离相等。
     • 对应点与旋转中心所连线段的夹角等于旋转角。
     • 旋转前后的图形全等。
   • 作图： 确定旋转中心、旋转方向和旋转角度，找出关键点的对应点，连接成新图形。

3. 中心对称

   • 定义： 如果一个图形绕着一个点旋转180°后能与另一个图形重合，那么这两个图形关于这个点成中心对称。
   • 性质： 关于中心对称的两个图形是全等图形，对称点所连线段都经过对称中心，并且被对称中心平分。
   • 中心对称图形： 一个图形绕某个点旋转180°后能与自身重合，这个图形就是中心对称图形（如平行四边形、圆等）。

第四章 一次函数

本章是初中函数的入门,是代数与几何结合的典范，也是中考的重点和难点。

1. 函数

   • 定义： 在一个变化过程中，有两个变量x和y，如果对于x的每一个值，y都有唯一确定的值与之对应，那么就说y是x的函数。
   • 自变量与因变量： x是自变量，y是因变量。

2. 正比例函数

   • 定义： 形如 y = kx (k≠0) 的函数。
   • 图像： 经过原点(0,0)和点(1,k)的一条直线。
   • 性质： 当k>0时，图像经过一、三象限，y随x的增大而增大；当k<0时，图像经过二、四象限，y随x的增大而减小。

3. 一次函数

   • 定义： 形如 y = kx + b (k≠0) 的函数。
   • 图像： 一条直线，可以看作是由正比例函数 y = kx 的图像向上或向下平移 |b| 个单位长度得到。
   • 性质：
     • 当k>0时，y随x的增大而增大；当k<0时，y随x的增大而减小。
     • 直线 y = kx + b 与y轴的交点为(0, b)，与x轴的交点为(-b/k, 0)。

4. 一次函数与方程、不等式的关系

   • 与方程： 一次函数 y = kx + b 的图像与x轴的交点的横坐标，就是方程 kx + b = 0 的解。
   • 与不等式：
     • 不等式 kx + b > 0 的解集，就是一次函数 y = kx + b 的图像在x轴上方部分对应的x的取值范围。
     • 不等式 kx + b < 0 的解集，就是一次函数 y = kx + b 的图像在x轴下方部分对应的x的取值范围。

5. 一次函数的应用

   • 图像法： 通过画函数图像解决实际问题，如行程问题、利润问题等。
   • 待定系数法： 已知两点坐标，求一次函数解析式的基本方法。

第五章 数据的分析

本章是统计学的内容,主要学习如何描述和整理一组数据的集中趋势和离散程度。

1. 平均数

   • 算术平均数： 所有数据之和除以数据的个数。
   • 加权平均数： 当数据的重要程度不同时，用“权”来衡量的平均数。加权平均数 = (x₁×w₁ + x₂×w₂ + ... + xₙ×wₙ) / (w₁ + w₂ + ... + wₙ)。

2. 中位数与众数

   • 中位数： 将一组数据从小到大排列，位于最中间位置的数（或最中间两个数的平均数），它不受极端值影响。
   • 众数： 一组数据中出现次数最多的数，一个数据集可以没有众数，也可以有多个众数。

3. 数据的波动程度

   • 极差： 一组数据中最大值与最小值的差，它反映数据的波动范围。
   • 方差： 各个数据与平均数差的平方的平均数，它更精确地描述数据的波动大小。
     • 方差越大,数据的波动越大，越不稳定。
     • 方差越小,数据的波动越小，越稳定。
   • 标准差： 方差的算术平方根，它的单位与原数据单位一致。

---

学习建议

1. 几何证明要严谨： 第一章是难点，务必掌握证明的格式和逻辑，每一步推理都要有理有据，不能凭感觉。
2. 数形结合是关键： 学习一次函数时，一定要多画图！通过图像理解函数的性质，将代数问题（方程、不等式）和几何问题（直线位置）联系起来。
3. 区分易混淆概念：
   • 不等式性质3,乘以或除以负数时，不等号方向要改变。
   • 一次函数 y = kx + b 中，k决定直线的倾斜方向和增减性，b决定直线与y轴的交点位置。
   • 方差和标准差都是衡量波动大小的,但标准差有单位。
4. 联系生活实际： 一次函数和数据分析的知识在现实生活中应用广泛，如购物优惠方案、比赛成绩评判等，尝试用数学知识解决这些问题，能加深理解。
5. 多做综合题： 八年级下册的知识综合性强，要多做一些将几何、代数、函数结合起来的题目，锻炼综合运用能力。

希望这份详细的概览能帮助你更好地学习和掌握北师大版八年级下册的数学知识！