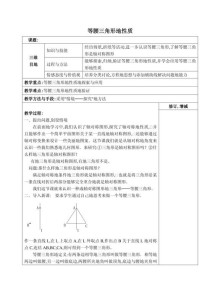
人教版8年级数学上册核心知识点有哪些?
校园之窗 2026年1月25日 23:45:36 99ANYc3cd6
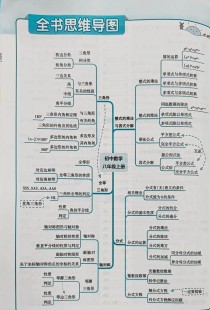
整体结构与核心内容
八年级上册的内容可以大致分为四个核心板块:
- 数与代数:主要学习实数和一次函数,这是从“有理数”到“实数”的扩展,也是函数学习的起点。
- 图形与几何:主要学习全等三角形和轴对称,这是初中几何证明的核心,是逻辑推理能力培养的关键。
- 统计与概率:主要学习数据的分析,从“描述数据”到“分析数据”,深化对数据的理解。
- 数学思想方法:贯穿全书的数形结合、转化与化归、分类讨论等思想方法。
各章节详细解析
第十一章 三角形
-
:
- 与三角形有关的线段:三角形的三边关系(两边之和大于第三边,两边之差小于第三边)、高、中线、角平分线。
- 与三角形有关的角:内角和定理(180°)、外角定理(等于不相邻两内角之和)。
- 多边形的内角和与外角和:n边形的内角和公式
(n-2)×180°,外角和恒为360°。
-
重点与难点:
- 重点:三角形三边关系的应用;三角形内角和定理的证明与应用。
- 难点:利用三角形三边关系判断三条线段能否构成三角形;解决与角有关的综合性计算题。
-
学习建议:
- 动手画图,理解三角形的基本元素和性质。
- 记住并熟练运用核心定理,这是后续几何证明的基础。
第十二章 全等三角形
-
:
- 全等三角形:能够完全重合的两个三角形。
- 全等三角形的性质:对应边相等,对应角相等。
- 判定公理/定理:
- 边边边
- 边角边
- 角边角
- 角角边
- 斜边、直角边 (仅用于直角三角形)
- 角平分线的性质:角平分线上的点到角两边的距离相等。
-
重点与难点:
- 重点:掌握五个全等判定方法,并能根据题目条件选择合适的方法来证明两个三角形全等。
- 难点:
- “对应”:准确找出全等三角形的对应边和对应角。
- 综合应用:利用全等证明线段相等、角相等、线段平行或垂直。
- 辅助线:学会添加适当的辅助线构造全等三角形(如倍长中线、截长补短等)。
-
学习建议:
- 这是几何证明的核心章节,必须高度重视。
- 多做证明题,总结证明思路,拿到题目后,先根据已知条件,思考可能用到的全等判定方法。
- 熟记常见的模型,如“手拉手模型”、“将军饮马模型”(雏形)等。
第十三章 轴对称
-
:
- 轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形。
- 轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全重合,那么就说这两个图形关于这条直线对称。
- 性质:对应点所连的线段被对称轴垂直平分;对应线段相等,对应角相等。
- 坐标中的轴对称:点
(x, y)x 轴对称的点是(x, -y),y 轴对称的点是(-x, y)。 - 等腰三角形:两腰相等,两底角相等(“等边对等角”)。
- 等边三角形:三边相等,三角都等于60°。
- 最短路径问题:将军饮马模型及其应用。
-
重点与难点:
- 重点:轴对称的性质;等腰三角形、等边三角形的性质和判定。
- 难点:
- 最短路径问题:这是典型的数形结合问题,需要将几何问题转化为代数问题(求线段和的最小值)。
- 等腰三角形的分类讨论(已知角求角,需判断是顶角还是底角)。
-
学习建议:
- 利用折纸等直观方式理解轴对称。
- 熟练掌握等腰三角形的“三线合一”(顶角平分线、底边上的中线、底边上的高互相重合)性质。
- 掌握“将军饮马”问题的基本模型和解题思路,这是中考热点。
第十四章 整式的乘法与因式分解
-
:
- 整式的乘法:
- 幂的运算性质(同底数幂相乘、幂的乘方、积的乘方)。
- 单项式乘以单项式、单项式乘以多项式、多项式乘以多项式。
- 乘法公式:平方差公式
(a+b)(a-b) = a² - b²,完全平方公式(a±b)² = a² ± 2ab + b²。
- 因式分解:
- 提公因式法。
- 公式法(平方差公式、完全平方公式)。
- 十字相乘法(用于二次三项式)。
- 整式的乘法:
-
重点与难点:
- 重点:幂的运算;乘法公式的灵活运用;因式分解的基本方法。
- 难点:
- 幂的运算混淆:容易将同底数幂相乘与幂的乘方混淆。
- 乘法公式的逆用:这是因式分解的基础,也是后续学习分式化简、解方程的关键。
- 综合因式分解:需要先提公因式,再用公式法或十字相乘法。
-
学习建议:
- 这部分是代数运算的基础,必须达到非常熟练的程度。
- 对比记忆幂的运算法则,多做练习,避免混淆。
- 因式分解要“彻底”,检查是否还能继续分解。
第十五章 分式
-
:
- 分式:形如
A/B(B中含有字母,且B≠0) 的式子。 - 基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。
- 运算:分式的乘除、分式的加减(同分母相加减,分母不变;异分母相加减,先通分变为同分母)。
- 整数指数幂:将负整数指数幂和零指数幂统一起来。
- 分式方程:分母中含有未知数的方程。
- 分式:形如
-
重点与难点:
- 重点:分式的基本性质;分式的四则运算;分式方程的解法。
- 难点:
- 分式的符号问题:分子、分母、分式本身的符号变化。
- 分式的通分:特别是异分母分式加减,找到最简公分母是关键。
- 分式方程的增根:解分式方程必须验根,检验的目的是看是否使原方程的最简公分母为0。
-
学习建议:
- 将分式运算与分数运算进行类比,理解其内在联系。
- 运算时细心,注意符号和通分步骤。
- 牢记解分式方程必须验根,这是易错点。
第十六章 二次根式
-
:
- 二次根式:形如
√a(a≥0) 的式子。 - 性质:
√(a²) = |a|;√(ab) = √a · √b(a≥0, b≥0);√(a/b) = √a / √b(a≥0, b>0)。 - 运算:
- 乘除:利用性质进行化简和计算。
- 加减:先将各根式化为最简二次根式,再合并被开方数相同的二次根式(同类二次根式)。
- 二次根式:形如
-
重点与难点:
- 重点:二次根式的性质;二次根式的四则运算。
- 难点:
√(a²) = |a|的理解与运用,特别是当a为负数时。- 二次根式的化简和混合运算,计算量较大,容易出错。
-
学习建议:
- 理解二次根式的定义(被开方数非负)。
- 掌握化简二次根式的方法,这是运算的基础。
- 运算时注意步骤清晰,避免跳步导致错误。
学习方法与建议
- 重视基础,回归课本:所有难题都是由基本概念、定理和公式组合而成的,确保对课本上的每一个定义、定理都理解透彻。
- 动手实践,多加练习:数学是“做”出来的,不是“看”出来的,特别是几何证明和代数运算,必须通过大量练习来巩固和熟练。
- 建立错题本,定期复习:准备一个错题本,记录做错的题目、错误原因和正确解法,定期回顾错题,避免重复犯错。
- 勤于思考,总结归纳:做完一道题后,不要只满足于答案,要思考这道题考查了哪些知识点?用了什么数学思想方法?有没有其他解法?对同类型的题目进行归纳总结,形成自己的解题套路。
- 培养数形结合思想:八年级上册的函数和几何内容特别适合数形结合,看到代数式,想想它的图像;看到几何图形,尝试用代数方法(如坐标系)去描述它。
- 寻求帮助,不懂就问:遇到难题时,先独立思考,如果实在无法解决,要及时向老师或同学请教,不要把问题堆积起来。
八年级上册是初中数学的“分水岭”,内容难度和学习要求都有显著提升,只要您能紧跟老师的教学节奏,掌握正确的学习方法,就一定能学好这一册的内容,为后续的学习打下坚实的基础,祝您学习进步!