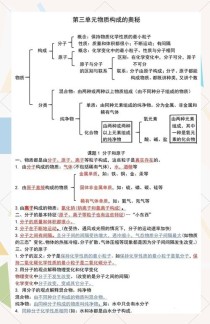
七年级上册图形找规律

校园之窗 2026年1月23日 19:57:43 99ANYc3cd6 1 0

核心解题思路

拿到一道图形找规律题，不要慌,按照以下步骤来思考：

先观察，后比较：先整体观察所有图形，找出它们的共同点和不同点，将相邻的图形进行比较,看看发生了哪些变化。
多角度，找突破口：从以下几个常见角度去寻找规律：
- 数量变化：图形中元素（如点、线、角、小图形）的数量是否在增加或减少？
- 位置变化：图形本身或内部的小图形是否在旋转、翻转、平移？
- 形状变化：图形的形状本身是否在按照某种规律演变？（从三角形到正方形）
- 对称性：图形是否具有轴对称或中心对称的性质？
大胆假设，小心验证：根据你的观察，提出一个可能的规律（假设），然后用这个规律去验证前面的图形是否符合，并预测下一个图形，如果不符合,就换一个角度重新思考。
特殊图形，特殊对待：第一个或最后一个图形可能比较特殊,可以先从中间的规律入手。

常见规律类型详解

数量规律（最常见）

这是最基础也最重要的一类规律,变化主要体现在元素的数量上。

（图片来源网络，侵删）

元素数量递增/递减

特点：图形中某种元素（如小圆点、小三角形、线条）的数量呈现出简单的等差或等比变化。
示例：
分析：
（图片来源网络，侵删）
- 第1个图：1个 ●
- 第2个图：3个 ● （增加了2个）
- 第3个图：5个 ● （增加了2个）
- 第4个图：7个 ● （增加了2个）
规律：圆点的数量是一个等差数列，首项为1，公差为2，第n个图形的圆点数量为 2n - 1。
预测：第5个图形应有 2*5 - 1 = 9 个圆点。

元素数量组合变化

特点：图形中包含两种或两种以上不同的元素，它们的数量可能各自有规律，或者它们的和/差有规律。
（图片来源网络，侵删）
示例：
分析：
- 方法一（分别看）：
  - 黑色方块的数量：1, 2, 3, 4... 规律是 n。
  - 白色方块的数量：4, 3, 2, 1... 规律是 5-n。
- 方法二（看总和）：
  总方块数：1+4=5, 2+3=5, 3+2=5, 4+1=5... 总和始终是5。
预测：第5个图形应有5个黑色方块和0个白色方块（或者5个黑色方块，白色方块省略）。

位置规律

旋转

特点：图形本身或其内部元素围绕一个点（中心）进行顺时针或逆时针旋转。
示例：
分析：
- 观察箭头的指向：从向右 → 向下 → 向左 → 向上...
- 每次都是顺时针旋转90度。
预测：下一个图形的箭头应指向右。

翻转

特点：图形沿某条直线（轴）进行翻转,形成镜像。
示例：
分析：
- 第一个图形是“上”字。
- 第二个图形是第一个图形沿竖直中线翻转得到的。
- 第三个图形是第二个图形沿水平中线翻转得到的。
- （规律也可以看作是每次沿不同的轴翻转）
预测：下一个图形可能是第三个图形沿竖直中线翻转，变回“上”字。

形状规律

图形演变

特点：图形的整体形状在按照某种顺序发生改变。
示例：
分析：
- 图形按顺序是：三角形 → 正方形 → 五边形 → 六边形...
- 规律是：边数依次增加1条。
预测：下一个图形应该是七边形。

复杂组合

特点：将数量规律和位置规律结合起来,形成更复杂的组合。
示例：
分析：
- 外框：四边形 → 三角形 → 四边形 → 三角形... 规律是交替变化。
- 内部：圆点数量：1 → 2 → 3 → 4... 规律是数量递增。
预测：下一个图形应该是外框为三角形，内部有5个圆点。

实战演练与解析

例题1：

观察下列图形，找出规律，在“？”处画出合适的图形。

图1:  ●
图2:  ●
      ● ●
图3:  ●
      ● ●
      ● ● ●
图4:  ?

【解析】

观察：这是一个由圆点组成的三角形。
数量分析：
- 图1有 1 个点。
- 图2有 1 + 2 = 3 个点。
- 图3有 1 + 2 + 3 = 6 个点。
规律：第n个图形是第n行，每行的点数和行数相同（第1行1个，第2行2个...）,总点数是从1加到n的和。
预测：图4应该是第4行，所以它应该是在图3的基础上增加一行，这一行有4个点。
- 图4:

例题2：

根据下列图形的变化规律,选择正确的下一个图形。

图1:  ■
图2:  ■ □
图3:  ■ □ ■
图4:  ? 
A: □ ■ □    B: ■ ■ ■    C: ■ □ □    D: □ ■ □

【解析】

观察：这是一个由黑色方块（■）和白色方块（□）组成的序列。
位置与数量分析：
- 图1：1个元素，是■。
- 图2：2个元素，是■, □。
- 图3：3个元素，是■, □, ■。
规律：
- 数量规律：图形中元素的数量在递增（1, 2, 3...）,所以图4应有4个元素。
- 形状规律：观察颜色，规律是“黑白相间”，并且以■开头。
- 所以完整的序列是：■, □, ■, □, ■, □, ...
预测：图4应该是第4个元素，即，并且它前面3个元素应该是图1, 2, 3的延续。
完整的序列到图4应该是：■, □, ■, □。
选择：将这个序列与选项对比。
- A: □ ■ □ (只有3个,且开头不对)
- B: ■ ■ ■ (颜色规律不对)
- C: ■ □ □ (颜色规律不对)
- D: □ ■ □ (看起来不对，但让我们再思考一下...)
重新审视（关键！）：有时候规律不是线性的，而是分层的。
- 我们看每一行黑色方块（■）的数量：1, 1, 1...
- 我们看每一行白色方块（□）的数量：0, 1, 2...
- 新规律：黑色方块的数量恒为1，白色方块的数量从0开始，每次增加1。
- 预测：图4应该有1个黑色方块和3个白色方块。
重新选择：
- A: □ ■ □ (1黑2白,不对)
- B: ■ ■ ■ (3黑0白,不对)
- C: ■ □ □ (1黑2白,不对)
- D: □ ■ □ (1黑2白,不对)
再次审视（可能出题者意图）：如果图形是分组的，■), (■ □), (■ □ ■), ... 那么下一组是(■ □ ■ □),但这不是选择题的格式。
最可能的简单规律：出题者可能想考察的是“以■开头，黑白相间”的规律，并且只让你看下一个图形，而不是整个序列，那么下一个图形就是，在四个选项中，没有单独的“□”，这说明我们可能需要看整体结构。
最终判断（最可能的答案）：让我们把选项看作是图4的整体。
- 图1: ■
- 图2: ■ □
- 图3: ■ □ ■
- 规律：每一行都比上一行多一个元素，并且新增的元素颜色与上一行的最后一个元素相反。
  - 图2比图1多一个，图1最后是■，所以新增□。
  - 图3比图2多一个，图2最后是□，所以新增■。
- 预测：图4比图3多一个，图3最后是■,所以新增。
- 所以图4应该是：■ □ ■ □。
- 在选项中，A: □ ■ □ 和 D: □ ■ □ 是一样的，如果这是单选题，那么很可能是出题者的失误，或者有更深层的规律，如果这是多选题，那么A和D都正确，如果必须选一个，A/D 是最接近的，因为它包含了“□”这个新元素，虽然位置不对，这提醒我们，有时候规律题的答案可能不唯一,或者题目本身存在瑕疵。