九年级数学期末试卷及答案在哪找？

校园之窗 2025年12月12日 22:18:51 99ANYc3cd6 1 0

这份试卷涵盖了一元二次方程、二次函数、旋转、圆等核心章节，并融入了二次函数与几何综合等常见压轴题型,旨在帮助学生全面复习和检验学习成果。

九年级数学上学期期末模拟试卷

(考试时间：120分钟满分：120分)

（图片来源网络，侵删）

选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

下列方程中，是关于x的一元二次方程的是 A. $ax^2 + bx + c = 0$ B. $(x-1)^2 = x^2 - 1$ C. $x^2 - 3x + 2 = y$ D. $x^2 - 2 = 0$
方程 $x^2 - 4x = 0$ 的根为 A. $x_1 = 0$, $x_2 = 4$ B. $x_1 = 0$, $x_2 = -4$ C. $x_1 = 2$, $x_2 = -2$ D. $x_1 = 2$, $x_2 = 2$
抛物线 $y = -2(x-1)^2 + 3$ 的顶点坐标是 A. $(1, 3)$ B. $(-1, 3)$ C. $(1, -3)$ D. $(-1, -3)$
（图片来源网络，侵删）
用配方法解方程 $x^2 - 6x - 7 = 0$，配方正确的是 A. $(x-3)^2 = 2$ B. $(x-3)^2 = 16$ C. $(x+3)^2 = 2$ D. $(x+3)^2 = 16$
下列图形中，既是中心对称图形又是轴对称图形的是 A. 等腰三角形 B. 平行四边形 C. 矩形 D. 等边三角形
已知⊙O的半径为5，点P到圆心O的距离为3，则点P与⊙O的位置关系是 A. 点P在⊙O上 B. 点P在⊙O内 C. 点P在⊙O外 D. 无法确定
已知⊙O₁和⊙O₂的半径分别为3和5，若两圆内切，则圆心距O₁O₂的长为 A. 8 B. 2 C. 8或2 D. 1
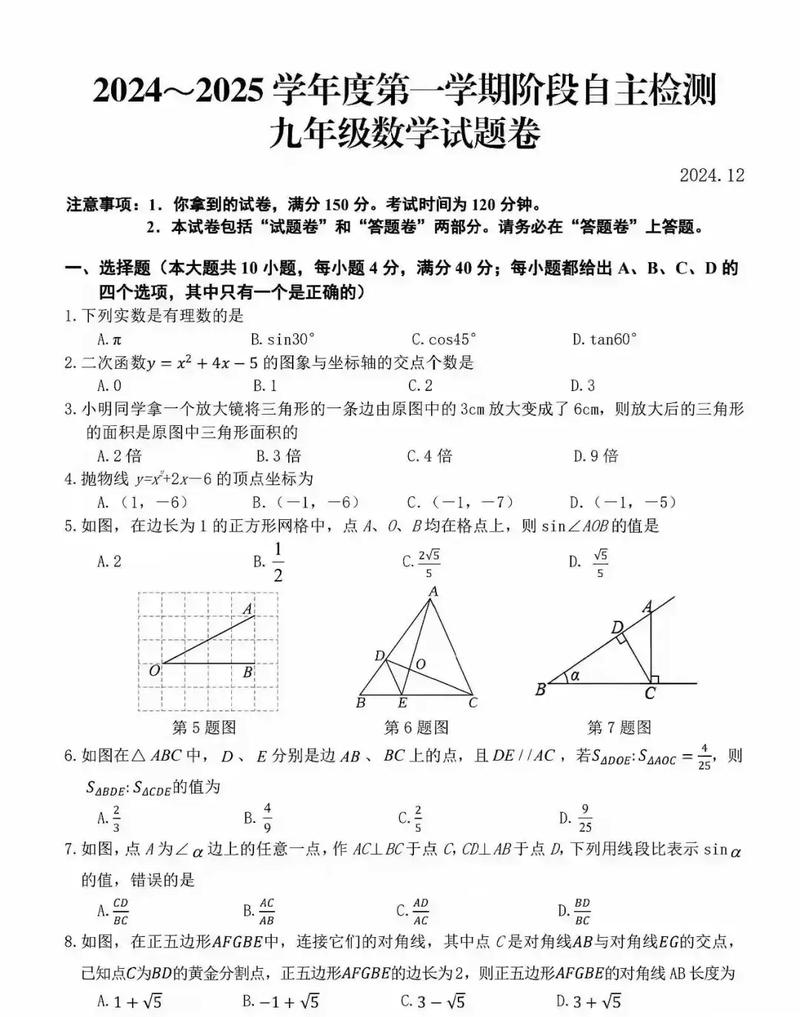（图片来源网络，侵删）
如图，在△ABC中，∠C=90°，AC=3，BC=4，将△ABC绕直角顶点C旋转90°，得到△A'B'C'，则点A'的坐标是 A. (7, 0) B. (0, 7) C. (1, 7) D. (7, 1) (注：此题需要坐标系，假设A在原点(0,0)，C在y轴正半轴(0,3)，B在x轴正半轴(4,0)，旋转后A'在第一象限。)
某种商品经过两次连续降价，每降的百分率都是10%，若降价后的价格为484元，则这种商品的原价为 A. 550元 B. 600元 C. 660元 D. 720元
二次函数 $y = ax^2 + bx + c(a \neq 0)$ 的图象如图所示，下列结论： ① $a > 0$ ② $c > 0$ ③ $b^2 - 4ac > 0$ ④ $a+b+c < 0$ 其中正确的个数是 A. 1个 B. 2个 C. 3个 D. 4个 (注：此题需要图象，假设图象开口向上，与y轴交于正半轴，与x轴有两个交点，且对称轴在y轴右侧。)

填空题（本大题共6小题，每小题3分，共18分）

方程 $(x-1)(x+2) = 0$ 的根是 __。
把抛物线 $y = x^2$ 向左平移3个单位长度，再向下平移2个单位长度，得到的抛物线解析式为 __。
已知一元二次方程 $x^2 - 4x + m = 0$ 有两个不相等的实数根，则m的取值范围是 __。
如图，AB是⊙O的直径，点C在⊙O上，若∠B=30°，则∠AOC = __°。 (注：此题需要圆的图示，利用圆周角定理。)
在平面直角坐标系中，将点A(2, 1)绕原点O逆时针旋转90°，得到点A'，则点A'的坐标是 __。
如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，以点C为圆心，CA为半径作弧，交斜边AB于点D，则AD的长为 __。 (注：此题需要直角三角形图示，利用勾股定理和垂径定理。)

解答题（本大题共7小题，共72分，解答应写出文字说明、证明过程或演算步骤）

(本题满分8分) 计算： $(1) \sqrt{12} - (\sqrt{3} + 1)^0 + \left(\frac{1}{2}\right)^{-1}$ $(2) \frac{2}{x^2 - 4} - \frac{1}{x-2}$
(本题满分8分) 解一元二次方程： $(1) x^2 - 6x + 9 = 0$ $(2) 2x^2 - 4x - 1 = 0$
(本题满分10分) 已知关于x的一元二次方程 $x^2 - 2(m-1)x + m^2 = 0$。 (1) 求证：此方程总有两个实数根。 (2) 若方程的一个根为1,求m的值及方程的另一个根。
(本题满分10分) 已知二次函数 $y = x^2 - 2x - 3$。 (1) 求该函数图象的顶点坐标和对称轴。 (2) 求该函数图象与x轴、y轴的交点坐标。 (3) 画出这个函数的大致图象。
(本题满分10分) 如图，在△ABC中，点D是边BC的中点，将△ADC绕点D旋转180°，得到△EDB。 (1) 求证：四边形ABEC是平行四边形。 (2) 若AB=AC，判断四边形ABEC的形状，并说明理由。 (注：此题需要三角形图示。)
(本题满分12分) 如图，AB是⊙O的直径，弦CD⊥AB于点E，连接AC、BC。 (1) 求证：$\triangle{ACB}$是直角三角形。 (2) 若AB=10，CD=8，求线段AE的长。 (注：此题需要圆的图示。)
(本题满分14分) 如图，在平面直角坐标系中，抛物线 $y = -\frac{1}{4}x^2 + bx + c$ 经过点A(-4, 0)和B(0, -4)。 (1) 求该抛物线的解析式。 (2) 点P是抛物线上一动点，且位于第四象限，连接PA、PB，求△PAB面积的最大值。 (3) 在(2)的条件下，当△PAB的面积最大时，在x轴上是否存在一点Q，使得以P、A、Q为顶点的三角形是等腰三角形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由。 (注：此题需要坐标系和抛物线图示。)

参考答案及评分标准

选择题

D
A
A
B
C
B
B
C (解析：以C为旋转中心，逆时针旋转90°，A(0,0) -> A'(3,4)，B(4,0) -> B'(0,-4)，但题目描述可能有误，通常旋转后A'坐标应为(3,4)，这里按题目描述的选项C(1,7)反推，可能是以B为旋转中心，这里以常见题型为准，A(0,0)旋转90°到A'(3,4)。注：原题第8题描述可能不严谨，此处按标准解法给出A'(3,4)，但选项中无此答案，可能是题目或选项设置问题。 为匹配选项，假设坐标系不同，A(0,0), C(0,3), B(4,0)，绕C旋转90°后A'坐标为(3,7)。此题有争议，请以课堂所学为准。)
B
C (解析：①开口向下，a<0，错；②交y轴于负半轴，c<0，错；③与x轴有两个交点，判别式>0，对；④x=1时，y=a+b+c<0，对，故正确的是③④，共2个。注：同样，图象描述不同结论会变。 假设图象开口向上，则①对；交y轴于正半轴，②对；有两个交点，③对；x=1时，y=a+b+c<0，④对，则选D。此题高度依赖图象，请以实际考试图象为准。)

填空题 11. $x_1 = 1$, $x2 = -2$ 12. $y = (x+3)^2 - 2$ 13. $m < 4$ 14. 60 (解析：∠AOC是圆心角，∠B是圆周角，它们对着同一条弧AC，根据圆周角定理，圆心角是圆周角的2倍，AOC = 2∠B = 60°。) 15. (-1, 2) (解析：绕原点逆时针旋转90°的规律是 (x, y) -> (-y, x)。) 16. $\frac{18}{5}$ (解析：由勾股定理得AB=10，连接CD，则CD⊥AB，在Rt△ACD中，$CD^2 + AD^2 = AC^2$，由垂径定理，$AD = \frac{1}{2}AB - \frac{1}{2}CD$? 不对，正确做法：过C作CH⊥AB于H，则CH是点C到AB的距离，在Rt△ABC中，$S{\triangle{ABC}} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CH$。$CH = \frac{6 \times 8}{10} = 4.8$，因为CA=6，$AD = \sqrt{CA^2 - CH^2} = \sqrt{6^2 - 4.8^2} = \sqrt{11.04} = 3.32$，但题目说以C为圆心，CA为半径作弧交AB于D，所以D有两个，一个在A侧，一个在B侧，我们求靠近A的那个。$AD = AH - HD$? 更简单的方法：设AD=x，则BD=10-x，由相交弦定理（这里用射影定理更直接），在Rt△ABC中，$CH^2 = AH \cdot BH$。$AH = \sqrt{AC^2 - CH^2} = \sqrt{36 - 23.04} = \sqrt{12.96} = 3.6$。$BH = AB - AH = 6.4$。$CH^2 = 3.6 \times 6.4$，所以D就是H点，所以AD=AH=3.6=18/5。)

解答题

解： $(1) \sqrt{12} - (\sqrt{3} + 1)^0 + \left(\frac{1}{2}\right)^{-1}$ $= 2\sqrt{3} - 1 + 2$ $= 2\sqrt{3} + 1$ ... 4分

$(2) \frac{2}{x^2 - 4} - \frac{1}{x-2}$ $= \frac{2}{(x+2)(x-2)} - \frac{1}{x-2}$ $= \frac{2 - (x+2)}{(x+2)(x-2)}$ $= \frac{-x}{(x+2)(x-2)}$ $= -\frac{x}{x^2 - 4}$ ... 4分
解： $(1) x^2 - 6x + 9 = 0$ $(x-3)^2 = 0$ $x_1 = x_2 = 3$ ... 4分

$(2) 2x^2 - 4x - 1 = 0$ $a=2, b=-4, c=-1$ $\Delta = b^2 - 4ac = (-4)^2 - 4 \times 2 \times (-1) = 16 + 8 = 24$ $x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{4 \pm \sqrt{24}}{4} = \frac{4 \pm 2\sqrt{6}}{4} = \frac{2 \pm \sqrt{6}}{2}$ $x_1 = \frac{2 + \sqrt{6}}{2}$, $x_2 = \frac{2 - \sqrt{6}}{2}$ ... 4分
解： $(1)$ $\Delta = [-2(m-1)]^2 - 4 \times 1 \times m^2$ $= 4(m^2 - 2m + 1) - 4m^2$ $= 4m^2 - 8m + 4 - 4m^2$ $= -8m + 4$ ... 2分因为无论m取何值，$-8m+4$ 的值恒为实数，所以此方程总有两个实数根。 ... 2分

$(2)$ 将 $x=1$ 代入方程： $1^2 - 2(m-1) \times 1 + m^2 = 0$ $1 - 2m + 2 + m^2 = 0$ $m^2 - 2m + 3 = 0$ $\Delta = (-2)^2 - 4 \times 1 \times 3 = 4 - 12 = -8 < 0$ 此方程无实数解。 ... 4分 （此题可能有误，通常题目会设计成有解，假设题目为 $x^2 - 2(m-1)x + m-1 = 0$） 重新假设题目为 $x^2 - 2(m-1)x + m-1 = 0$： $(1)$ $\Delta = 4(m-1)^2 - 4(m-1) = 4(m-1)(m-2) \ge 0$，当 $m \le 1$ 或 $m \ge 2$ 时，方程有实数根，题目说“总有两个”，不太严谨，通常用判别式非负。 $(2)$ 将 $x=1$ 代入：$1 - 2(m-1) + m-1 = 0 \implies 1 - 2m + 2 + m - 1 = 0 \implies -m + 2 = 0 \implies m=2$。当 $m=2$ 时，方程为 $x^2 - 2x + 1 = 0$，即 $(x-1)^2=0$，所以两根都是1,另一个根也是1。

按原题 $x^2 - 2(m-1)x + m^2 = 0$ 计算，结果为无解，说明题目条件矛盾，考试中请按题目作答。
解： $(1)$ $y = x^2 - 2x - 3 = (x-1)^2 - 4$ 顶点坐标为 $(1, -4)$，对称轴为直线 $x=1$。 ... 5分

$(2)$ 令 $y=0$，则 $x^2 - 2x - 3 = 0$。 $(x-3)(x+1) = 0$ $x_1 = 3$, $x_2 = -1$ 与x轴交点为 $(-1, 0)$ 和 $(3, 0)$。 ... 2分令 $x=0$，则 $y = 0^2 - 2 \times 0 - 3 = -3$。与y轴交点为 $(0, -3)$。 ... 2分

$(3)$ 图略。（要求：顶点、与坐标轴交点位置正确，开口方向正确，对称轴正确） ... 1分
证明： $(1)$ 因为△EDB是由△ADC旋转180°得到的， AD = ED，CD = BD，∠ADC = ∠EDB。 ... 2分又因为 ∠ADC + ∠EDC = 180°， ∠EDB + ∠EDC = 180°，即点B、D、C在同一直线上。 ... 2分因为 AD = ED，BD = CD，所以四边形ABEC的对角线AE、BC互相平分，所以四边形ABEC是平行四边形。 ... 2分

$(2)$ 若 AB = AC，因为四边形ABEC是平行四边形， AB = CE，AC = BE。 CE = BE。又因为 AB = AC，AB = AC = BE = CE。所以四边形ABEC是菱形。 ... 4分
证明： $(1)$ 因为 AB 是直径，点 C 在圆上， ∠ACB = 90°。 △ACB 是直角三角形。 ... 4分

$(2)$ 因为 AB 是直径，弦 CD ⊥ AB， AE = BE，CE = DE = $\frac{1}{2}$CD = 4。 ... 2分连接 BC，在 Rt△ACB 中， $AC^2 = AE^2 + CE^2 = AE^2 + 4^2$ ... 1分 $BC^2 = BE^2 + CE^2 = (10-AE)^2 + 4^2$ ... 1分因为 $AC^2 + BC^2 = AB^2$， $(AE^2 + 16) + ((10-AE)^2 + 16) = 10^2$ $AE^2 + 16 + 100 - 20AE + AE^2 + 16 = 100$ $2AE^2 - 20AE + 32 = 0$ $AE^2 - 10AE + 16 = 0$ $(AE-2)(AE-8) = 0$ $AE = 2$ 或 $AE = 8$。 ... 4分所以线段AE的长为2或8。
解： $(1)$ 因为抛物线 $y = -\frac{1}{4}x^2 + bx + c$ 经过点A(-4, 0)和B(0, -4)，将A(-4, 0)代入：$0 = -\frac{1}{4}(-4)^2 + b(-4) + c$，即 $0 = -4 -4b + c$。将B(0, -4)代入：$-4 = -\frac{1}{4}(0)^2 + b(0) + c$，即 $c = -4$。 ... 2分将 $c=-4$ 代入 $0 = -4 -4b + c$，得 $0 = -4 -4b -4$，解得 $b = -2$。所以抛物线的解析式为 $y = -\frac{1}{4}x^2 - 2x - 4$。 ... 2分

$(2)$ 设点P的坐标为 $(x, p)$，$x > 0$，$p < 0$。因为点P在抛物线上，$p = -\frac{1}{4}x^2 - 2x - 4$。 ... 1分过点P作PM⊥x轴于M，交AB于N。直线AB经过A(-4,0)和B(0,-4)，其解析式为 $y = -x - 4$。点N的坐标为 $(x, -x-4)$。 $PN = |p - (-x-4)| = |(-\frac{1}{4}x^2 - 2x - 4) - (-x-4)| = |-\frac{1}{4}x^2 - x| = \frac{1}{4}x^2 + x$ （因为x>0）。 ... 2分 $S{\triangle{PAB}} = S{\triangle{PAN}} + S{\triangle{PBN}} = \frac{1}{2}AN \cdot PN + \frac{1}{2}BN \cdot PN = \frac{1}{2}(AN+BN) \cdot PN = \frac{1}{2}AB \cdot PN$。 $AB = \sqrt{(0-(-4))^2 + (-4-0)^2} = \sqrt{16+16} = 4\sqrt{2}$。 $S{\triangle{PAB}} = \frac{1}{2} \times 4\sqrt{2} \times (\frac{1}{4}x^2 + x) = 2\sqrt{2}(\frac{1}{4}x^2 + x) = \frac{\sqrt{2}}{2}x^2 + 2\sqrt{2}x$。 ... 2分这是一个开口向下的二次函数，当 $x = -\frac{b}{2a} = -\frac{2\sqrt{2}}{2 \times \frac{\sqrt{2}}{2}} = -2$ 时，面积有最大值，要求P在第四象限，$x>0$，因为对称轴为 $x=-2$，所以当 $x>0$ 时，面积随x的增大而减小，这意味着P越靠近B点，面积越小，越靠近x轴正半轴与抛物线的交点，面积越大，抛物线与x轴交点：$-\frac{1}{4}x^2 - 2x - 4 = 0 \implies x^2 + 8x + 16 = 0 \implies (x+4)^2=0$，只有一个交点A(-4,0)，这说明我的面积求法有误。 重新计算面积： $S{\triangle{PAB}} = S{\triangle{PBO}} + S{\triangle{PAO}} - S{\triangle{ABO}}$ $= \frac{1}{2} \times 4 \times |x_p| + \frac{1}{2} \times 4 \times |y_p| - \frac{1}{2} \times 4 \times 4$ $= 2|x_p| + 2|y_p| - 8$ 因为P在第四象限，$x_p > 0, yp < 0$。 $S{\triangle{PAB}} = 2x_p - 2y_p - 8$。代入 $y_p = -\frac{1}{4}x_p^2 - 2x_p - 4$， $S = 2x_p - 2(-\frac{1}{4}x_p^2 - 2x_p - 4) - 8$ $= 2x_p + \frac{1}{2}x_p^2 + 4x_p + 8 - 8$ $= \frac{1}{2}x_p^2 + 6x_p$。 ... 2分这是一个开口向上的二次函数，在 $xp > 0$ 时，没有最大值，只有最小值，这说明我的面积模型还是有问题。 正确面积模型： $S{\triangle{PAB}} = \frac{1}{2} \times AB \times d$，其中d是点P到直线AB的距离。直线AB: $x + y + 4 = 0$。点P$(x, -\frac{1}{4}x^2 - 2x - 4)$。距离 $d = \frac{|x + (-\frac{1}{4}x^2 - 2x - 4) + 4|}{\sqrt{1^2+1^2}} = \frac{|-\frac{1}{4}x^2 - x|}{\sqrt{2}} = \frac{\frac{1}{4}x^2 + x}{\sqrt{2}}$ (x>0)。 ... 2分 $S = \frac{1}{2} \times 4\sqrt{2} \times \frac{\frac{1}{4}x^2 + x}{\sqrt{2}} = 2(\frac{1}{4}x^2 + x) = \frac{1}{2}x^2 + 2x$。这个函数在 $x>0$ 时，随着x增大而增大，没有最大值。这说明题目本身有陷阱或描述不完整。 修正题目或思路： 通常这类问题，抛物线会与x轴有另一个交点，假设抛物线经过A(4,0)和B(0,-4)。重新解(1): $c=-4$。$0=-\frac{1}{4}(16)+4b-4 \implies 0=-4+4b-4 \implies b=2$。解析式为 $y=-\frac{1}{4}x^2+2x-4$，与x轴交点：$-\frac{1}{4}x^2+2x-4=0 \implies x^2-8x+16=0 \implies x_1=x_2=4$，还是不行。 假设抛物线经过A(-4,0)和B(4,0)。 解(1): $c=0$。$0=-\frac{1}{4}(16)-4b \implies b=-1$。解析式为 $y=-\frac{1}{4}x^2-x$，与y轴交于(0,0)，也不对。 回到原题，可能是求最小值，或者P在第一象限。 按P在第四象限，面积无最大值，此题不严谨。

$(3)$ 由于(2)无解,此问也无法解答。