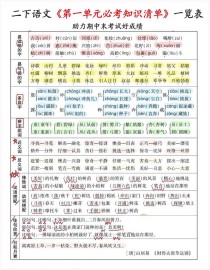
九年级上册数学二次函数

下面我将从知识体系、核心概念、图像与性质、典型应用、学习方法五个方面为你进行详细讲解。

---

知识体系概览

二次函数的知识点可以看作一个“金字塔”：

• 基础（塔基）：定义、表达式（一般式、顶点式、交点式）
• 核心（塔身）：图像（抛物线）及其性质（开口方向、顶点、对称轴、增减性、最值）
• 应用（塔尖）：与一元二次方程/不等式的关系、实际问题建模（最值问题）、二次函数与几何图形的综合题

---

核心概念详解

定义

一般地,形如 y = ax² + bx + c (a, b, c是常数，a ≠ 0) 的函数，叫做二次函数。

• 关键点：a 必须不为 0。a=0，函数就变成了 y = bx + c，是一次函数。
• 自变量：x
• 因变量：y

表达式（三种形式）

表达式形式	名称	特点与作用
y = ax² + bx + c	一般式	最直接的函数形式，便于进行代数运算和求值。
y = a(x - h)² + k	顶点式	非常重要！ 直接显示抛物线的顶点坐标是 (h, k)，对称轴是直线 x = h，便于研究函数最值和图像平移。
y = a(x - x₁)(x - x₂)	交点式	非常重要！ 直接显示抛物线与 x 轴的交点坐标是 (x₁, 0) 和 (x₂, 0)，便于求方程的根和画草图。

三种形式之间的转化：

• 一般式 → 顶点式：通过配方法完成。
• 一般式 → 交点式：通过因式分解法或求根公式法先求出与 x 轴的交点。
• 顶点式/交点式 → 一般式：通过去括号、合并同类项完成。

---

图像与性质（重中之重）

二次函数的图像是一条抛物线，所有性质都由 a, b, c 这三个系数决定。

抛物线的基本性质

性质	决定因素	描述
开口方向	系数 a	a > 0：开口向上；a < 0：开口向下。
开口大小	|a| 的大小	|a| 越大，开口越窄；|a| 越小，开口越宽。
顶点坐标	a, b, c	一般式：顶点坐标为 (-b/2a, (4ac-b²)/4a) 顶点式：顶点坐标为 (h, k)
对称轴	a, b	一般式：对称轴是直线 x = -b/2a 顶点式：对称轴是直线 x = h
与 y 轴交点	常数项 c	与 y 轴交于点 (0, c)。
与 x 轴交点	b² - 4ac (判别式)	令 y=0，解方程 ax² + bx + c = 0。 Δ = b² - 4ac - Δ > 0：有两个交点 (x₁, 0) 和 (x₂, 0) - Δ = 0：有一个交点（顶点在 x 轴上）(x₁, 0) - Δ < 0：无交点

函数的增减性

• 当 a > 0 时（开口向上）：
  • 在对称轴 左侧 (x < -b/2a)，y 随着 x 的增大而减小。
  • 在对称轴 右侧 (x > -b/2a)，y 随着 x 的增大而增大。
• 当 a < 0 时（开口向下）：
  • 在对称轴 左侧 (x < -b/2a)，y 随着 x 的增大而增大。
  • 在对称轴 右侧 (x > -b/2a)，y 随着 x 的增大而减小。

函数的最值

• 当 a > 0 时（开口向上）：
  • 函数有最小值。
  • 最小值 = 顶点的纵坐标 = (4ac-b²)/4a。
  • x 的值为 -b/2a。
• 当 a < 0 时（开口向下）：
  • 函数有最大值。
  • 最大值 = 顶点的纵坐标 = (4ac-b²)/4a。
  • x 的值为 -b/2a。

---

典型应用

二次函数与一元二次方程/不等式的关系

关系	描述	方法
与方程的关系	二次函数 y = ax² + bx + c 的图像与 x 轴的交点的横坐标，就是对应的一元二次方程 ax² + bx + c = 0 的实数根。	画图看交点，或计算判别式 。
与不等式的关系	ax² + bx + c > 0 (或 < 0) 的解集，就是抛物线 y = ax² + bx + c 在 x 轴上方（或下方）的点的横坐标的取值范围。	口诀：大于取两边，小于取中间（前提是 a>0 且有两个交点），画图是最佳方法！

实际问题建模（最值问题）

这是二次函数最常见的应用题类型,通常步骤如下：

1. 审题：理解题意，找出题目中的变量（通常一个是自变量 x，一个是因变量 y）。
2. 找关系：根据题意，用含有 x 的代数式表示 y，得到函数关系式 y = ax² + bx + c。
3. 求最值：
   • 将关系式化为顶点式 y = a(x-h)² + k。
   • 根据 a 的正负判断是最大值还是最小值。
   • 最值就是 k，并求出对应的 x 值。
4. 答：根据题目要求，写出完整的答案。

常见模型：

• 面积问题（如矩形面积、窗格面积等）。
• 利润问题（利润 = 单价 × 销量 - 成本）。
• 几何图形中的动点问题。

二次函数与几何图形的综合

这是中考的压轴题形式,综合性强，通常会将二次函数与三角形、四边形、圆等几何知识结合起来，考查面积、相似、全等等。

核心思路：

• 数形结合：充分利用函数图像的几何意义。
• 方程思想：通过解方程组求交点坐标。
• 转化思想：将不规则图形的面积转化为规则图形（如三角形、梯形）的和或差。

---

学习方法与建议

1. 抓牢核心，理解本质：始终围绕 a, b, c 对图像和性质的影响来学习。a 决定“胖瘦”和“方向”，b 和 a 共同决定“对称轴”，c 决定“与 y 轴交点”。

   
   （图片来源网络，侵删）

2. 数形结合，画图先行：遇到二次函数的题目，尤其是求不等式解集、比较函数值大小、求交点等问题时，先画草图，一个准确的草图能帮你直观地解决问题，避免很多错误。

3. 掌握三种形式的转化：熟练掌握配方法和因式分解法，这是二次函数的基本功，根据题目需要，灵活选择函数表达式形式，求最值用顶点式，求根用交点式，其他运算用一般式。

4. 建立联系，融会贯通：将二次函数与一元二次方程、不等式、几何图形紧密联系起来，看到 b²-4ac，要立刻想到它和抛物线与 x 轴交点个数的关系。

5. 分类讨论，严谨思考：在涉及最值、不等式解集等问题时，一定要讨论 a 的正负，以及抛物线与 x 轴交点个数（即 的情况），这是保证答案全面、不遗漏的关键。

6. 勤加练习，总结反思：多做不同类型的题目，特别是实际应用题和综合题，做完题后，要反思解题思路，总结题型和方法，形成自己的知识体系。

希望这份详细的梳理能帮助你更好地理解和掌握二次函数！祝你学习进步！